
科目: 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】对于数列![]() ,把
,把![]() 作为新数列
作为新数列![]() 的第一项,把
的第一项,把![]() 或
或![]() (
(![]() )作为新数列
)作为新数列![]() 的第
的第![]() 项,数列
项,数列![]() 称为数列
称为数列![]() 的一个生成数列.例如,数列
的一个生成数列.例如,数列![]() 的一个生成数列是
的一个生成数列是![]() .已知数列
.已知数列![]() 为数列
为数列![]() 的生成数列,
的生成数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)写出![]() 的所有可能值;
的所有可能值;
(2)若生成数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:对于给定的![]() ,
,![]() 的所有可能值组成的集合为
的所有可能值组成的集合为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题p:实数![]() 满足不等式
满足不等式![]() ;
;
命题q:关于![]() 不等式
不等式![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x2-ax)ex(x∈R),a为实数.
(1)当a=0时,求函数f(x)的单调增区间;
(2)若f(x)在闭区间[-1,1]上为减函数,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了获得更大的收益,每年要投入一定的资金用于广告促销,经调查,每年投入广告费t百万元,可增加销售额约为![]() 百万元.
百万元.
(Ⅰ)若该公司将一年的广告费控制在4百万元之内,则应投入多少广告费,才能使该公司由此增加的收益最大?
(Ⅱ)现该公司准备共投入5百万元,分别用于广告促销和技术改造,经预测,每投入技术改造费![]() 百万元,可增加的销售额约为
百万元,可增加的销售额约为![]() 百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
(注:收益=销售额-投入,这里除了广告费和技术改造费,不考虑其他的投入)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取一名,抽到第二批次中女职工的概率是0.16.
第一批次 | 第二批次 | 第三批次 | |
女教职工 | 196 |
|
|
男教职工 | 204 | 156 |
|
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3)已知![]() ,
,![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
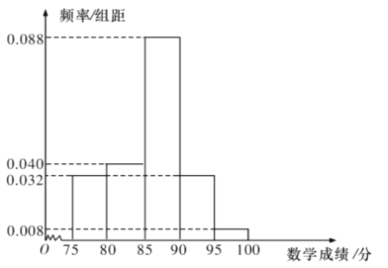
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②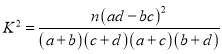 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com