【题目】如图，上海迪士尼乐园将一三角形地块的一角开辟为游客体验活动区，已知，、的长度均大于米，设，，且、总长度为米.

（1）当、为何值时，游客体验活动区的面积最大，并求最大面积？

（2）当、为何值时，线段最小，并求最小值？

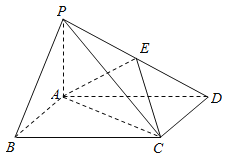
(1) 证明：PB∥平面AEC

(2) 设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积

【题目】在平面直角坐标系xOy中，曲线C的参数方程为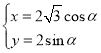，其中为参数，在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，点P的极坐标为，直线l的极坐标方程为.

（1）求曲线C的普通方程与直线l的直角坐标方程；

（2）若Q是曲线C上的动点，M为线段PQ的中点，求点M到直线l的距离的最大值.

【题目】作为交通重要参与者的行人，闯红灯通行频有发生，带来了较大的交通安全隐患.在某十字路口，交警部门从穿越该路口的行人中随机抽取了200人进行调查，得到不完整的列联表如图所示：

（1）将列联表补充完整；

（2）是否有99.9%的把握认为行人是否闯红灯与年龄有关.

参考公式及数据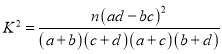：，其中.

【题目】已知抛物线：，过其焦点作斜率为1的直线交抛物线于，两点，且线段的中点的纵坐标为4.

（1）求抛物线的标准方程；

（2）若不过原点且斜率存在的直线与抛物线相交于、两点，且.求证：直线过定点，并求出该定点的坐标.

【题目】设是定义在R上的两个周期函数，的周期为4，的周期为2，且是奇函数.当时，，，其中k>0.若在区间(0，9]上，关于x的方程有8个不同的实数根，则k的取值范围是_____.

【题目】已知为定义在实数集上的函数，把方程称为函数的特征方程，特征方程的两个实根、（），称为的特征根.

（1）讨论函数的奇偶性，并说明理由；

（2）已知为给定实数，求的表达式；

（3）把函数，的最大值记作，最小值记作，研究函数，的单调性，令，若恒成立，求的取值范围.

【题目】已知圆，椭圆的短半轴长等于圆的半径，且过右焦点的直线与圆相切于点．

（1）求椭圆的方程；

（2）若动直线与圆相切，且与相交于两点，求点到弦的垂直平分线距离的最大值．

【题目】已知函数（）.

（1）求证：函数是增函数；

（2）若函数在上的值域是（），求实数的取值范围；

（3）若存在，使不等式成立，求实数的取值范围.

【题目】有甲、乙二人去看望高中数学张老师，期间他们做了一个游戏，张老师的生日是月日，张老师把告诉了甲，把告诉了乙，然后张老师列出来如下10个日期供选择: 2月5日，2月7日，2月9日，3月2日，3月7日，5月5日，5月8日，7月2日，7月6日，7月9日．看完日期后，甲说“我不知道，但你一定也不知道”，乙听了甲的话后，说“本来我不知道，但现在我知道了”，甲接着说，“哦，现在我也知道了”．请问张老师的生日是_______．