
科目: 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
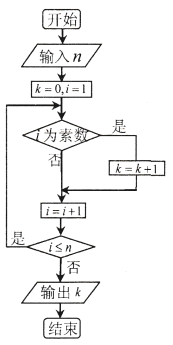
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]() 到焦点
到焦点![]() 的距离等于3.
的距离等于3.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业为了提高企业利润,从2014年至2018年每年都对生产环节的改进进行投资,投资金额![]() (单位:万元)与年利润增长量
(单位:万元)与年利润增长量![]() (单位:万元)的数据如表:
(单位:万元)的数据如表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
年利润增长量 | 6.0 | 7.0 | 9.0 | 11.0 | 12.0 |
(1)记![]() 年利润增长量
年利润增长量![]() 投资金额,现从2014年至2018年这5年中抽出两年进行调查分析,求所抽两年都是
投资金额,现从2014年至2018年这5年中抽出两年进行调查分析,求所抽两年都是![]() 万元的概率;
万元的概率;
(2)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该企业对生产环节改进的投资金额为10万元,试估计该企业在2019年的年利润增长量为多少?
的回归直线方程;如果2019年该企业对生产环节改进的投资金额为10万元,试估计该企业在2019年的年利润增长量为多少?
参考公式: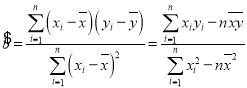 ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
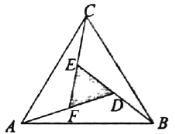
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成).类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( ).
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求续驶里程在![]() 的车辆数;
的车辆数;
(2)求续驶里程的平均数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若存在常数![]() ,使得对定义域D内的任意两个不同的实数
,使得对定义域D内的任意两个不同的实数![]() ,均有:
,均有:![]() 成立,则称
成立,则称![]() 在D上满足利普希茨(Lipschitz)条件.
在D上满足利普希茨(Lipschitz)条件.
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数![]() 的值,并加以验证;
的值,并加以验证;
(2)若函数![]() 在
在![]() 上满足利普希茨(Lipschitz)条件,求常数
上满足利普希茨(Lipschitz)条件,求常数![]() 的最小值;
的最小值;
(3)现有函数![]() ,请找出所有的一次函数
,请找出所有的一次函数![]() ,使得下列条件同时成立:
,使得下列条件同时成立:
①函数![]() 满足利普希茨(Lipschitz)条件;
满足利普希茨(Lipschitz)条件;
②方程![]() 的根
的根![]() 也是方程
也是方程![]() 的根,且
的根,且![]() ;
;
③方程![]() 在区间
在区间![]() 上有且仅有一解.
上有且仅有一解.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校进入高中数学竞赛复赛的学生中,高一年级有8人,高二年级有16人,高三年级有32人,现釆用分层抽样的方法从这些学生中抽取7人进行釆访.
(1)求应从各年级分别抽取的人数;
(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为![]() ,高二学生记为
,高二学生记为![]() ,高三学生记为
,高三学生记为![]() ,
,![]()
①列出所有可能的抽取结果;
②求抽取的2人均为高三年级学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com