
科目: 来源: 题型:
【题目】无穷数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,
,![]() ,记
,记![]() (
(![]() 表示3个实数
表示3个实数![]() 、
、![]() 、
、![]() 中的最大数).
中的最大数).
(1)若![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求满足条件
时,求满足条件![]() 的
的![]() 的取值范围;
的取值范围;
(3)证明:对于任意正整数![]() 、
、![]() 、
、![]() ,必存在正整数
,必存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
附: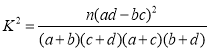 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】把半椭圆![]() (
(![]() )与圆弧
)与圆弧![]() (
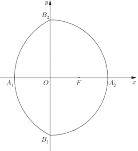
(![]() )合成的曲线称作“曲圆”,其中
)合成的曲线称作“曲圆”,其中![]() 为
为![]() 的右焦点,如图所示,
的右焦点,如图所示,![]() 、
、![]() 、
、![]() 、
、![]() 分别是“曲圆”与
分别是“曲圆”与![]() 轴、
轴、![]() 轴的交点,已知
轴的交点,已知![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线交“曲圆”于
的直线交“曲圆”于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴的上方).
轴的上方).
(1)求半椭圆![]() 和圆弧
和圆弧![]() 的方程;
的方程;
(2)当点![]() 、
、![]() 分别在第一、第三象限时,求△
分别在第一、第三象限时,求△![]() 的周长
的周长![]() 的取值范围;
的取值范围;
(3)若射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交“曲圆”于点
交“曲圆”于点![]() ,请用
,请用![]() 表示
表示![]() 、
、![]() 两点的坐标,并求△
两点的坐标,并求△![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,直线l过点P(1,1),且倾斜角α=![]() .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取![]() 件产品作为样本称出它们的质量(单位:毫克),质量值落在
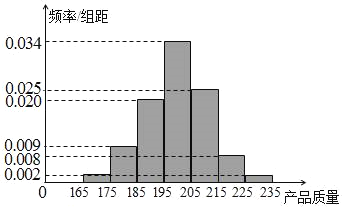
件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)以样本的频率作为概率,试估计从甲流水线上任取![]() 件产品,求其中不合格品的件数
件产品,求其中不合格品的件数![]() 的数学期望.
的数学期望.
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅱ)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
(Ⅲ)由乙流水线的频率分布直方图可以认为乙流水线生产的产品质量![]() 服从正态分布
服从正态分布![]() ,求质量
,求质量![]() 落在
落在![]() 上的概率.
上的概率.
参考公式:![]()
![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
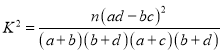 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入![]() 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员
万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员![]() 名(
名(![]() 且
且![]() ),调整后研发人员的年人均投入增加
),调整后研发人员的年人均投入增加![]() %,技术人员的年人均投入调整为
%,技术人员的年人均投入调整为![]() 万元.
万元.
(1)要使这![]() 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
(2)是否存在这样的实数![]() ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出
,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程是![]() (
(![]() 为参数),把曲线C的横坐标缩短为原来的
为参数),把曲线C的横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() 直线l的普通方程是
直线l的普通方程是![]() ,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求直线l的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() (
(![]() )与
)与![]() 交于点A,与l交于点B,求
交于点A,与l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】十七世纪,法国数学家费马提出猜想;“当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 没有正整数解”,经历三百多年,1995年英国数学家安德鲁
没有正整数解”,经历三百多年,1995年英国数学家安德鲁![]() 怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
①对任意正整数![]() ,关于
,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 都没有正整数解;
都没有正整数解;
②当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
③当正整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
④若关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解,则正整数
至少存在一组正整数解,则正整数![]() ;
;
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 的在数集
的在数集![]() 上都有定义,对于任意的
上都有定义,对于任意的![]() ,当
,当![]() 时,
时,![]() 或
或![]() 成立,则称
成立,则称![]() 是数集
是数集![]() 上
上![]() 的限制函数.
的限制函数.
(1)求![]() 在
在![]() 上的限制函数
上的限制函数![]() 的解析式;
的解析式;
(2)证明:如果![]() 在区间
在区间![]() 上恒为正值,则
上恒为正值,则![]() 在
在![]() 上是增函数;[注:如果
上是增函数;[注:如果![]() 在区间
在区间![]() 上恒为负值,则
上恒为负值,则![]() 在区间
在区间![]() 上是减函数,此结论无需证明,可以直接应用]
上是减函数,此结论无需证明,可以直接应用]
(3)利用(2)的结论,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com