【题目】关于函数，，下列说法正确的是（ ）

A.当时，在处的切线方程为

B.当时，存在唯一极小值点，且

C.对任意，在上均存在零点

D.存在，在上有且只有一个零点

【题目】如图，在棱长为1的正方体中，分别为棱的中点.为面对角线上任一点，则下列说法正确的是（ ）

A.平面内存在直线与平行

B.平面截正方体所得截面面积为

C.直线和所成角可能为60°

D.直线和所成角可能为30°

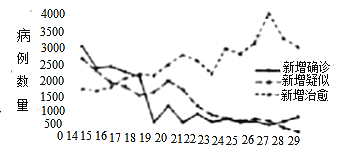
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大

B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数

C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000

D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和

①命题：“已知 ，“”是“”的充分不必要条件”；

②命题：“p且q为真”是“p或q为真”的必要不充分条件；

③命题：已知幂函数的图象经过点（2，），则f（4）的值等于；

④命题：若，则．

A. 1B. 2C. 3D. 4

年级组为了解学生的体质，随机抽取了100名学生的跳绳个数作为一个样本，绘制了如下样本频率分布直方图.

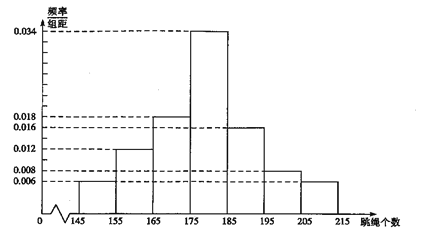
（1）现从样本的100名学生跳绳个数中，任意抽取2人的跳绳个数，求两人得分之和小于35分的概率；（用最简分数表示）

（2）若该校高二年级共有2000名学生，所有学生的一分钟跳绳个数近似服从正态分布，其中，为样本平均数的估计值（同一组中数据以这组数据所在区间中点值作代表）.利用所得的正态分布模型，解决以下问题：

（i）估计每分钟跳绳164个以上的人数（结果四舍五入到整数）；

（ii）若在全年级所有学生中随机抽取3人，每分钟跳绳在179个以上的人数为，求随机变量的分布列和数学期望与方差.

附：若随机变量服从正态分布，则，，.

【题目】已知函数（），是的导数.

（1）当时，令，为的导数.证明：在区间存在唯一的极小值点；

（2）已知函数在上单调递减，求的取值范围.

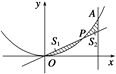
(1)当S1＝S2时，求点P的坐标；

(2)当S1＋S2有最小值时，求点P的坐标和最小值．

【题目】如图，在直角中，，通过以直线为轴顺时针旋转得到（）.点为斜边上一点.点为线段上一点，且.

（1）证明：平面；

（2）当直线与平面所成的角取最大值时，求二面角的正弦值.

（1）完成列联表（应适当写出计算过程）；

（2）试运用独立性检验的思想方法分析是否有的把握认为学生的学习成绩与善于总结反思有关.

统计数据如下表所示：

参考公式：其中

若分数不低于95分，则称该员工的成绩为“优秀”.

（1）从这20人中任取3人，求恰有1人成绩“优秀”的概率；

（2）根据这20人的分数补全下方的频率分布表和频率分布直方图，并根据频率分布直方图解决下面的问题.

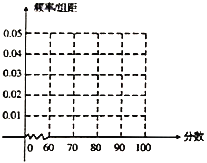
①估计所有员工的平均分数（同一组中的数据用该组区间的中点值作代表）；

②若从所有员工中任选3人，记表示抽到的员工成绩为“优秀”的人数，求的分布列和数学期望.