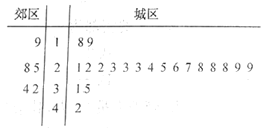
（1）若在郊区的这5户居民中随机抽取2户，求“被抽取的2户年人均用水量的和超过60吨”的概率；

（2）若该城市郊区和城区的居民户数比为1：5，现将年人均用水量不超过30吨的用户定义为第一阶梯用户，只保证这一梯次的居民用户用水价格不变，试根据样本估计总体的思想分析此方案是否符合国家“保基本”政策．

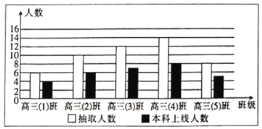
（1）根据条形统计图，估计本届高三学生本科上线率.

（2）已知该省甲市2020届高考考生人数为4万，假设以（1）中的本科上线率作为甲市每个考生本科上线的概率.

（i）若从甲市随机抽取10名高三学生，求恰有8名学生达到本科线的概率（结果精确到0.01）；

（ii）已知该省乙市2020届高考考生人数为3.6万，假设该市每个考生本科上线率均为，若2020届高考本科上线人数乙市的均值不低于甲市，求p的取值范围.

可能用到的参考数据：取，.

【题目】已知函数f(x)＝ln (x＋1)－ －x，a∈R.

(1)当a>0时，求函数f(x)的单调区间；

(2)若存在x>0，使f(x)＋x＋1<－ (a∈Z)成立，求a的最小值．

【题目】已知函数.

（1）求函数的单调区间和极值；

（2）设定义在上的函数的最大值为，最小值为，且，求实数的取值范围.

【题目】已知椭圆过点，且离心率为.

（1）求椭圆的方程；

（2）已知圆方程为，过圆上任意一点作圆的切线，切线与椭圆交于，两点，为坐标原点，设为的中点，求的取值范围.

【题目】已知椭圆过点，且焦距为4

（1）求椭圆的标准方程：

（2）设为直线上一点，为椭圆上一点.以为直径的圆恒过坐标原点.

(i)求的取值范围

(ii)是否存在圆心在原点的定圆恒与直线相切？若存在，求出该定圆的方程；若不存在，说明理由.

【题目】已知函数.

（1）若在上恒成立，求的取值范围，并证明：对任意的，都有

（2）设.讨论方程实数根的个数

（1）从该社区随机抽取一名居民参与问卷测试，试估计其得分不低于60分的概率；

（2）将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类，完成列联表，并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关？

（3）从参与问卷测试且得分不低于80分的居民中，按照性别进行分层抽样，共抽取10人，连同名男性调查员一起组成3个环保宜传队.若从这中随机抽取3人作为队长，且男性队长人数占的期望不小于2.求的最小值.

附：

临界值表：

【题目】如图，三棱锥中，点分别是的中点，点是的重心.

（1）证明：平面；

（2）若平面平面，，，，，求平面与平面所成的锐二面角的余弦值.