
科目: 来源: 题型:
【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: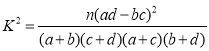
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下图是民航部门统计的某年春运期间,六个城市售出的往返机票的平均价格(单位元),以及相比于上一年同期价格变化幅度的数据统计图,以下叙述不正确的是( )
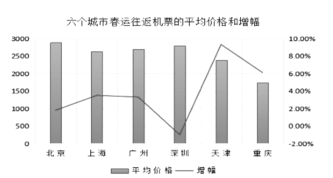
A.深圳的变化幅度最小,北京的平均价格最高
B.天津的往返机票平均价格变化最大
C.上海和广州的往返机票平均价格基本相当
D.相比于上一年同期,其中四个城市的往返机票平均价格在增加
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,某省由于人员流动性较大,成为湖北省外疫情最严重的省份之一,截至2月29日,该省已累计确诊1349例患者(无境外输入病例).
(1)为了解新冠肺炎的相关特征,研究人员从该省随机抽取100名确诊患者,统计他们的年龄数据,得下面的频数分布表:
年龄 |
|
|
|
|
|
|
|
|
|
人数 | 2 | 6 | 12 | 18 | 22 | 22 | 12 | 4 | 2 |
由频数分布表可以大致认为,该省新冠肺炎患者的年龄![]() 服从正态分布img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中
服从正态分布img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中![]() 近似为这100名患者年龄的样本平均数(同一组中的数据用该组区间的中点值作代表).请估计该省新冠肺炎患者年龄在70岁以上(
近似为这100名患者年龄的样本平均数(同一组中的数据用该组区间的中点值作代表).请估计该省新冠肺炎患者年龄在70岁以上(![]() )的患者比例;
)的患者比例;
(2)截至2月29日,该省新冠肺炎的密切接触者(均已接受检测)中确诊患者约占10%,以这些密切接触者确诊的频率代替1名密切接触者确诊发生的概率,每名密切接触者是否确诊相互独立.现有密切接触者20人,为检测出所有患者,设计了如下方案:将这20名密切接触者随机地按![]() (
(![]() 且
且![]() 是20的约数)个人一组平均分组,并将同组的
是20的约数)个人一组平均分组,并将同组的![]() 个人每人抽取的一半血液混合在一起化验,若发现新冠病毒,则对该组的
个人每人抽取的一半血液混合在一起化验,若发现新冠病毒,则对该组的![]() 个人抽取的另一半血液逐一化验,记
个人抽取的另一半血液逐一化验,记![]() 个人中患者的人数为
个人中患者的人数为![]() ,以化验次数的期望值为决策依据,试确定使得20人的化验总次数最少的
,以化验次数的期望值为决策依据,试确定使得20人的化验总次数最少的![]() 的值.
的值.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示双曲线.
1(m∈R)表示双曲线.
(1)若p为真命题,求m的取值范围;
(2)若p∨q为真,p∧q为假,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )

A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 在定义域内极值点的个数;
在定义域内极值点的个数;
(2)设直线![]() 为函数
为函数![]() 的图象上一点
的图象上一点![]() 处的切线,证明:在区间
处的切线,证明:在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 左、右顶点分别为A、B,上顶点为D(0,1),离心率为
左、右顶点分别为A、B,上顶点为D(0,1),离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)若点E是椭圆C上位于x轴上方的动点,直线AE、BE与直线![]() 分别交于M、N两点,当线段MN的长度最小时,椭圆C上是否存在点T使
分别交于M、N两点,当线段MN的长度最小时,椭圆C上是否存在点T使![]() 的面积为
的面积为![]() ?若存在,求出点T的坐标:若不存在,请说明理由.
?若存在,求出点T的坐标:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
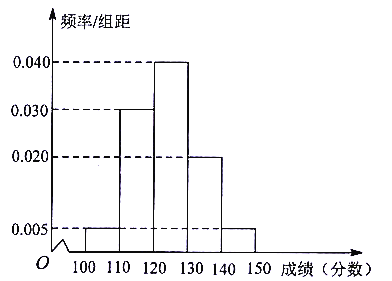
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com