
科目: 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 和点
和点![]() ,动点
,动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹曲线
的轨迹曲线![]() 的方程并说明
的方程并说明![]() 是何种曲线;
是何种曲线;
(2)若抛物线![]() :
:![]() 的焦点
的焦点![]() 恰为曲线
恰为曲线![]() 的顶点,过点
的顶点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-5:不等式选讲
已知f(x)=|x+a|(a∈R).
(1)若f(x)≥|2x﹣1|的解集为[0,2],求a的值;
(2)若对任意x∈R,不等式f(x)+|x﹣a|≥3a﹣2恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,该椭圆的左顶点A到直线
上,该椭圆的左顶点A到直线![]() 的距离为
的距离为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 若线段MN平行于y轴,满足
若线段MN平行于y轴,满足![]() ,动点P在直线
,动点P在直线![]() 上,满足
上,满足![]() 证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B. “![]() 且
且![]() 为真命题”是“
为真命题”是“![]() 或
或![]() 为真命题” 的必要不充分条件
为真命题” 的必要不充分条件
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命题![]() :“
:“![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x3-2x2+x+a,g(x)=-2x+![]() ,若对任意的x1∈[-1,2],存在x2∈[2,4],使得f(x1)=g(x2),则实数a的取值范围是________.
,若对任意的x1∈[-1,2],存在x2∈[2,4],使得f(x1)=g(x2),则实数a的取值范围是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间( | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数( | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
(1)若选取的是后面4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过35人,试用(1)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: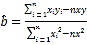
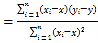 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com