
科目: 来源: 题型:
【题目】某中学要举行元旦晚会,要求每班各出一个节目,其中高二年级一班学生中,有3名学生只会跳舞,有2名学生只会唱歌.
(I)求从上述5人中选出一人会唱歌的概率;
(II)写出该班出一个舞蹈节目的所有基本事件.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点在坐标轴上.
(1)若抛物线C经过点![]() ,求C的标准方程;
,求C的标准方程;
(2)抛物线C的焦点![]() (m是大于零的常数),若过点F的直线与C交于
(m是大于零的常数),若过点F的直线与C交于![]()
![]() 两点,
两点,![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
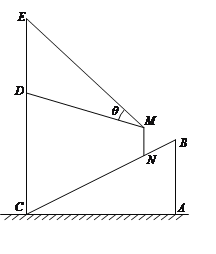
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高![]() 为
为![]() 米,它所占水平地面的长
米,它所占水平地面的长![]() 为
为![]() 米.该广告画最高点
米.该广告画最高点![]() 到地面的距离为
到地面的距离为![]() 米,最低点
米,最低点![]() 到地面距离
到地面距离![]() 米.假设某人眼睛到脚底的距离
米.假设某人眼睛到脚底的距离![]() 为
为![]() 米,他竖直站在此电梯上观看
米,他竖直站在此电梯上观看![]() 视角为
视角为![]() .
.
(Ⅰ)设此人到直线![]() 的距离为
的距离为![]() 米,试用含
米,试用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)此人到直线![]() 的距离为多少米时,视角
的距离为多少米时,视角![]() 最大?
最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在直角梯形中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到如图②所示的几何体.
,得到如图②所示的几何体.
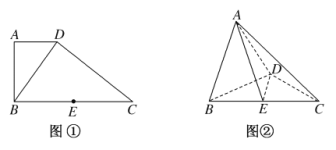
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与
且与![]() 轴相切,点
轴相切,点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)一条直线经过点![]() ,且交曲线
,且交曲线![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 为直线
为直线![]() 上的动点.
上的动点.
①求证:![]() 不可能是钝角;
不可能是钝角;
②是否存在这样的点![]() ,使得
,使得![]() 是正三角形?若存在,求点
是正三角形?若存在,求点![]() 的坐标:否则,说明理由.
的坐标:否则,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的![]() ,男生喜欢抖音的人数占男生人数的
,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() 若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
查看答案和解析>>
科目: 来源: 题型:
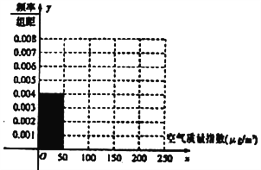
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 上顶点为
上顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,圆
,圆![]() :
:![]() 与直线
与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三个动点,直线
上的三个动点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() .
.
(i)若![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(ii)若![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com