
科目: 来源: 题型:
【题目】已知函数![]() ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定![]() 的单调区间:
的单调区间:
(II)若f(x)在区间![]() (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中重要的一部分,其中大学生更是频频使用网络外卖服务.![]() 市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了
市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了![]() 人,并将这
人,并将这![]() 人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过
人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过![]() 元):
元):
消费金额(单位:百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
![]() 由频数分布表可以认为,该市大学生网络外卖消费金额
由频数分布表可以认为,该市大学生网络外卖消费金额![]() (单位:元)近似地服从正态分布
(单位:元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值,
(每组数据取区间的中点值,![]() ).现从该市任取
).现从该市任取![]() 名大学生,记其中网络外卖消费金额恰在
名大学生,记其中网络外卖消费金额恰在![]() 元至
元至![]() 元之间的人数为
元之间的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
![]()
![]() 市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值
市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值![]() 元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第
元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第![]() 格、第
格、第![]() 格、第
格、第![]() 格、…、第
格、…、第![]() 格共
格共![]() 个方格.棋子开始在第
个方格.棋子开始在第![]() 格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是
格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是![]() ,其中
,其中![]() ),若掷出正面,将棋子向前移动一格(从
),若掷出正面,将棋子向前移动一格(从![]() 到
到![]() ),若掷出反面,则将棋子向前移动两格(从
),若掷出反面,则将棋子向前移动两格(从![]() 到
到![]() ).重复多次,若这枚棋子最终停在第
).重复多次,若这枚棋子最终停在第![]() 格,则认为“闯关成功”,并赠送
格,则认为“闯关成功”,并赠送![]() 元充值饭卡;若这枚棋子最终停在第
元充值饭卡;若这枚棋子最终停在第![]() 格,则认为“闯关失败”,不再获得其他奖励,活动结束.
格,则认为“闯关失败”,不再获得其他奖励,活动结束.
①设棋子移到第![]() 格的概率为
格的概率为![]() ,求证:当
,求证:当![]() 时,
时,![]() 是等比数列;
是等比数列;
②若某大学生参与这档“闯关游戏”,试比较该大学生闯关成功与闯关失败的概率大小,并说明理由.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 在抛物线
在抛物线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,动点
,动点![]() 满足
满足![]() .
.
![]() 求动点
求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
![]() 过点
过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,记
,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,问:
,问:![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】若直线![]() 与曲线
与曲线![]() 满足以下两个条件:点
满足以下两个条件:点![]() 在曲线
在曲线![]() 上,直线
上,直线![]() 方程为
方程为![]() ;曲线
;曲线![]() 在点
在点![]() 附近位于直线
附近位于直线![]() 的两侧,则称直线
的两侧,则称直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() .下列选项正确的是( )
.下列选项正确的是( )
A.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
B.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
C.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
D.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】中央电视台为了解一档诗歌节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如茎叶图所示:其中一个数字被污损.
个城市,得到观看该节目的人数(单位:千人)如茎叶图所示:其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)现从观看该节目的观众中随机统计了![]() 位观众的周均学习诗歌知识的时间
位观众的周均学习诗歌知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如表所示):由表中数据,求线性回归方程
(单位:岁),并制作了对照表(如表所示):由表中数据,求线性回归方程![]() ,并预测年龄在
,并预测年龄在![]() 岁的观众周均学习诗歌知识的时间.
岁的观众周均学习诗歌知识的时间.

年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
(参考数据:![]() ,回归直线方程参考公式:
,回归直线方程参考公式: )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为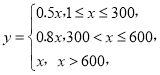
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com