【题目】四棱锥中，平面，底面为菱形，且有，，是线段上一点，且与所成角的正弦值是.

（1）求的大小；

（2）若与平面所成的角的正弦值是，求的值.

附：

根据表格计算得的观测值，据此判断下列结论正确的是（ ）

A.没有任何把握认为“手机品牌的选择与年龄大小有关”

B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”

C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”

D.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小无关”

【题目】已知一组样本点，其中.根据最小二乘法求得的回归方程是，则下列说法正确的是（ ）

A. 若所有样本点都在上，则变量间的相关系数为1

B. 至少有一个样本点落在回归直线上

C. 对所有的预报变量，的值一定与有误差

D. 若斜率，则变量与正相关

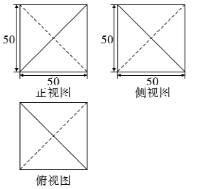
【题目】祖冲之是中国南北朝时期的数学家和天文学家，他在数学方面的突出贡献是将圆周率的精确度计算到小数点后第位，也就是和之间，这一成就比欧洲早了多年，我校“爱数学”社团的同学，在祖冲之研究圆周率的方法启发下，自制了一套计算圆周率的数学实验模型.该模型三视图如图所示，模型内置一个与其各个面都相切的球，该模型及其内球在同一方向有开口装置.实验的时候，同学们随机往模型中投掷大小相等，形状相同的玻璃球，通过计算落在球内的玻璃球数量，来估算圆周率的近似值.已知某次实验中，某同学一次投掷了个玻璃球，请你根据祖冲之的圆周率精确度（取小数点后三位）估算落在球内的玻璃球数量（ ）

A.B.C.D.

（1）若从统计的5年中任取2年，求这2年的垃圾处理量至少有一年不低于8.0（千万吨）的概率；

（2）由表中数据求得线性回归方程为，该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨，现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元，请你预测2017年能否完成垃圾处理任务，若不能，缺口约为多少千万吨？

【题目】有三张形状、大小、质地完全一致的卡片，在每张卡片上写上0，1，2，现从中任意抽取一张，将其上数字记作x，然后放回，再抽取一张，其上数字记作y，令.求：

（1）所取各值的分布列；

（2）随机变量的数学期望与方差.

某商场经销某商品，根据以往资料统计，顾客采用的付款期数的分布列为

商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元.表示经销一件该商品的利润.

（Ⅰ）求事件A：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率

P(A)；

（Ⅱ）求的分布列及期望

(1)设所选3人中女生人数为ξ，求ξ的分布列；

(2)求男生甲或女生乙被选中的概率；

(3)设“男生甲被选中”为事件A，“女生乙被选中”为事件B，求P(B)和P(B|A)．

【题目】在平面直角坐标系中，已知曲线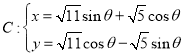（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为：.

（1）求直线和曲线的直角坐标方程；

（2），直线和曲线交于、两点，求的值.

【题目】近几年市加大雾霾治理的投入，空气质量与前几年相比有了很大改善，并于年市入选中国空气优良城市.已知该市设有个监测站用于监测空气质量指数（），其中在轻度污染区、中度污染区、重度污染区分别设有、、个监测站，并以个监测站测得的的平均值为依据播报该市的空气质量.

（1）若某日播报的为，已知轻度污染区平均值为，中度污染区平均值为，求重度污染区平均值；

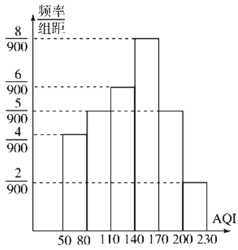
（2）如图是年月份天的的频率分布直方图，月份仅有天在内.

①某校参照官方公布的，如果周日小于就组织学生参加户外活动，以统计数据中的频率为概率，求该校学生周日能参加户外活动的概率；

②环卫部门从月份不小于的数据中抽取两天的数据进行研究，求抽取的这两天中值在的天数的概率.