【题目】已知函数．

（1）若时，直线与函数图象有三个相异的交点，求实数的取值范围；

（2）讨论的单调性．

【题目】在平面直角坐标系中，已知抛物线的焦点为，准线为，是抛物线上上一点，且点的横坐标为，.

（1）求抛物线的方程；

（2）过点的直线与抛物线交于、两点，过点且与直线垂直的直线与准线交于点，设的中点为，若、、四点共圆，求直线的方程.

【题目】已知函数在处有极值．

（1）求的解析式；

（2）若关于的不等式恒成立，求实数的取值范围．

【题目】若养殖场每个月生猪的死亡率不超过，则该养殖场考核为合格，该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示：

（1）从该养殖场2019年2月到6月这5个月中任意选取3个月，求恰好有2个月考核获得合格的概率；

（2）根据1月到8月的数据，求出月利润y（十万元）关于月养殖量x（千只）的线性回归方程（精确到0.001）.

（3）预计在今后的养殖中，月利润与月养殖量仍然服从（2）中的关系，若9月份的养殖量为1.5万只，试估计：该月利润约为多少万元？

附：线性回归方程中斜率和截距用最小二乘法估计计算公式如下：，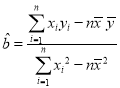

参考数据：.

【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入,则输出的结果是( )

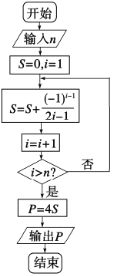
A.B.

C.D.

【题目】在平面直角坐标系中，曲线（为参数），在以原点为极点，轴正半轴为极轴的极坐标系中，曲线.

（1）写出的普通方程和的直角坐标方程；

（2）设点在曲线上，点在曲线上，求的最小值及此时点的直角坐标.

【题目】已知椭圆的短轴长为，离心率，其右焦点为.

（1）求椭圆的方程；

（2）过作夹角为的两条直线分别交椭圆于和，求的取值范围.

【题目】已知函数.

（1）讨论函数的极值；

（2）是否存在实数，使得不等式在上恒成立？若存在，求出的最小值：若不存在，请说明理由.

【题目】已知椭圆：的短轴长为，离心率为.

（1）求椭圆的方程；

（2）求过椭圆的右焦点且倾斜角为135°的直线，被椭圆截得的弦长；

（3）若直线与椭圆相交于，两点（不是左右顶点），且以为直径的圆过椭圆的右顶点，求证：直线过定点，并求出该定点的坐标．

【题目】已知函数．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）求函数的单调区间；

（Ⅲ）若对任意的，都有成立，求a的取值范围．