
科目: 来源: 题型:
【题目】抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() .②
.②![]() 的面积
的面积![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,问题中的
这三个条件中任选一个,补充在下面问题中,问题中的![]() 是否为等边三角形,请说明理由.在
是否为等边三角形,请说明理由.在![]() 中,
中,![]() 分别为内角
分别为内角![]() 的对边,且
的对边,且![]() ,________,试判断
,________,试判断![]() 是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
科目: 来源: 题型:
【题目】从中国教育在线官方公布的考研动机调查来看,本科生扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力;通过考研选择真正感兴趣的专业;为了获得学历;继续深造;随大流;有名校情结.如图是2015~2019年全国硕士研究生报考人数趋势图(单位:万人)的拆线图.
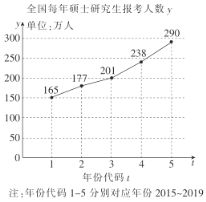
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,预测2021年全国硕士研究生报考人数.
参考数据:![]() ;
;
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为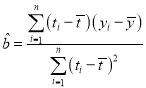 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,
,![]() ,恰为等比数列
,恰为等比数列![]() 的前3项.
的前3项.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)求数列 的前
的前![]() 项和为
项和为![]() ;若对
;若对![]() 均满足
均满足![]() ,求整数
,求整数![]() 的最大值;
的最大值;
(3)是否存在数列![]() 满足等式
满足等式![]() 成立,若存在,求出数列
成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,且过点
的焦距为2,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为
为![]() 的左焦点,点
的左焦点,点![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于两点
于两点![]() ,
,![]()
(ⅰ)证明:![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(ⅱ)当![]() 取最小值时,求点
取最小值时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ∥BC,
∥BC,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
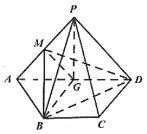
(1)若![]() ,
,
(ⅰ)求证:PC∥平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(2)否存在实数![]() 满足
满足![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,若存在,确定的
,若存在,确定的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】4月23日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取12名学生参加问卷调查.各组人数统计如下:
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用![]() 表示抽得甲组学生的人数,求随机变量
表示抽得甲组学生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com