
科目: 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 是否满足
是否满足![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生 450 人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含女生45人,求
名学生中含女生45人,求![]() 的值及抽取到的男生人数;
的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取的选择“地理”的学生中按分层抽样再抽取6名,再从这6名学生中抽取2人了解学生对“地理”的选课意向情况,求2人中至少有1名男生的概率.

| 0.05 | 0.01 |
| 3.841 | 6.635 |
参考公式:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某研究性学习小组对无现金支付(支付宝、微信、银行卡)的用户进行问卷调查,随机选取了![]() 人(图1),按年龄分为青年组与中老年组,如图2.
人(图1),按年龄分为青年组与中老年组,如图2.
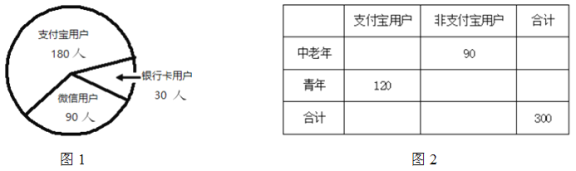
(1)完成图2的列联表,并判断是否有![]() 的把握认为使用支付宝用户与年龄有关系?
的把握认为使用支付宝用户与年龄有关系?
(2)现从调查的中老年组中按分层抽样的方法选出![]() 人,再随机抽取
人,再随机抽取![]() 人赠送礼品,试求抽取的
人赠送礼品,试求抽取的![]() 人中恰有
人中恰有![]() 人为“非支付宝用户”的概率.
人为“非支付宝用户”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某手机企业为确定下一年度投入某种产品的研发费用,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 千万元与年销售量
千万元与年销售量![]() 千万件的数据,得到散点图1,对数据作出如下处理:令
千万件的数据,得到散点图1,对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如图2:
,得到相关统计量的值如图2:

(1)利用散点图判断![]() 和
和![]()
![]() 哪一个更适合作为年研发费用
哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归类型(不必说明理由),并根据数据,求出
的回归类型(不必说明理由),并根据数据,求出![]() 与
与![]() 的回归方程;
的回归方程;
(2)已知企业年利润![]() 千万元与
千万元与![]() 的关系式为
的关系式为![]() (其中
(其中![]() 为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
查看答案和解析>>
科目: 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产甲、乙两种产品,销售利润分别为2千元/件、1千元/件.甲、乙两种产品都需要在![]() 两种设备上加工,生产一件甲产品需用
两种设备上加工,生产一件甲产品需用![]() 设备2小时,
设备2小时, ![]() 设备6小时;生产一件乙产品需用
设备6小时;生产一件乙产品需用![]() 设备3小时,
设备3小时, ![]() 设备1小时.
设备1小时. ![]() 两种设备每月可使用时间数分别为480小时、960小时,若生产的产品都能及时售出,则该企业每月利润的最大值为( )
两种设备每月可使用时间数分别为480小时、960小时,若生产的产品都能及时售出,则该企业每月利润的最大值为( )
A. 320千元 B. 360千元 C. 400千元 D. 440千元
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
① 函数![]() 的最小正周期是
的最小正周期是![]() ;
;
② 函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③ 函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
④ 函数![]() 的图像可由函数
的图像可由函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再向下平移1个单位得到.其中正确结论的个数是( )
个单位,再向下平移1个单位得到.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且满足:
且满足:![]()
(1)证明:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,若数列
,若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)在(2)的条件下,设![]() 记数列
记数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 存在实数
存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com