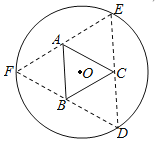
【题目】如图，圆形纸片的圆心为，半径为，该纸片上的等边三角形的中心为.，，为圆上的点，分别是以为底边的等腰三角形.沿虚线剪开后，分别以为折痕折起，使得，，重合，得到三棱锥.当所得三棱锥体积（单位：）最大时，的边长为_________（）.

【题目】已知平面直角坐标系中，过点的直线的参数方程为（t为参数），与y轴交于A，以该直角坐标系的原点O为极点，轴的非负半轴为极轴建立极坐标系.曲线C的极坐标方程，直线与曲线C交于M、N两点.

（1）求曲线C的直角坐标方程和点A的一个极坐标；

（2）若，求实数m的值.

【题目】国庆70周年阅兵式上的女兵们是一道靓丽的风景线，每一名女兵都是经过层层筛选才最终入选受阅方队，筛选标准非常严格，例如要求女兵身高（单位：cm）在区间内.现从全体受阅女兵中随机抽取200人，对她们的身高进行统计，将所得数据分为，，，，五组，得到如图所示的频率分布直方图，其中第三组的频数为75，最后三组的频率之和为0.7.

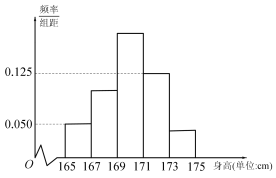
（1）请根据频率分布直方图估计样本的平均数和方差（同一组中的数据用该组区间的中点值代表）；

（2）根据样本数据，可认为受阅女兵的身高X（cm）近似服从正态分布，其中近似为样本平均数，近似为样本方差.

（i）求；

（ii）若从全体受阅女兵中随机抽取10人，求这10人中至少有1人的身高在174.28cm以上的概率.

参考数据：若，则，，，，，.

【题目】已知函数．

（1）若，求函数的最大值；

（2）令，讨论函数的单调区间；

（3）若，正实数满足，证明：

【题目】某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为、、、、五个等级，统计数据如图所示（视频率为概率），根据图中抽样调查的数据，回答下列问题：

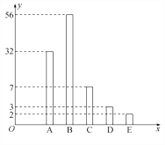
（1）试估算该校高三年级学生获得成绩为的人数；

（2）若等级、、、、分别对应100分、90分、80分、70分、60分，学校要求当学生获得的等级成绩的平均分大于90分时，高三学生的考前心理稳定，整体过关，请问该校高三年级目前学生的考前心理稳定情况是否整体过关？

（3）以每个学生的心理都培养成为健康状态为目标，学校决定对成绩等级为的16名学生（其中男生4人，女生12人）进行特殊的一对一帮扶培训，从按分层抽样抽取的4人中任意抽取2名，求恰好抽到1名男生的概率..

【题目】已知函数是R上的奇函数，当时，，则函数在上的所有零点之和为（ ）

A.0B.4C.8D.16

（1）为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关，现随机选取了一部分社区居民进行调查，其中被调查的男性居民和女性居民人数相同，男性居民中不喜欢担任垃圾分类志愿者占男性居民的，女性居民中不喜欢担任垃圾分类志愿者占女性居民的，若研究得到在犯错误概率不超过0.010的前提下，认为居民喜欢担任垃圾分类志愿者与性别有关，则被调查的女性居民至少多少人？

附，，

（2）某垃圾站的日垃圾分拣量（千克）与垃圾分类志愿者人数（人）满足回归直线方程，数据统计如下：

已知，，，根据所给数据求和回归直线方程，附：，．

（3）用（2）中所求的线性回归方程得到与对应的日垃圾分拣量的估计值．当分拣数据与估计值满足时，则将分拣数据称为一个“正常数据”．现从5个分拣数据中任取3个，记表示取得“正常数据”的个数，求的分布列和数学期望．

【题目】已知函数

（1）当时，求不等式的解集；

（2）若函数的值域为A，且，求a的取值范围.

【题目】在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为.

（1）求直线l的普通方程和圆C的直角坐标方程；

（2）直线l与圆C交于A，B两点，点P(2,1)，求|PA||PB|的值.

(1)求ξ，η的分布列；

(2)求ξ，η的数学期望与方差，并以此比较甲、乙的射击技术．