
科目: 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
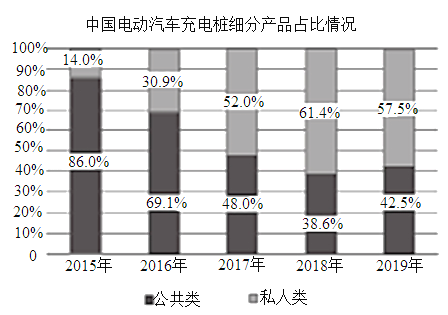
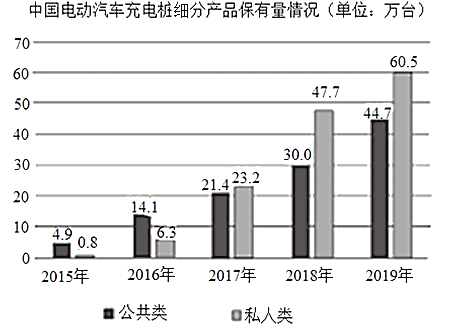
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (t为参数),以坐标原点为极点,
(t为参数),以坐标原点为极点,![]() 正半轴为极轴,建立极坐标系,曲线
正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 距离的最小值,并求出此时
距离的最小值,并求出此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】西安市自2017年5月启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,斑马线前礼让行人也成为了一张新的西安“名片”.
但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患及机动车通畅率降低,交警部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到![]() 列联表如下:
列联表如下:
30岁以下 | 30岁以上 | 合计 | |
闯红灯 | 60 | ||
未闯红灯 | 80 | ||
合计 | 200 |
近期,为了整顿“行人闯红灯”这一不文明及项违法行为,交警部门在该十字路口试行了对闯红灯行人进行经济处罚,并从试行经济处罚后穿越该路口行人中随机抽取了200人进行调查,得到下表:
处罚金额 | 5 | 10 | 15 | 20 |
闯红灯的人数 | 50 | 40 | 20 | 0 |
将统计数据所得频率代替概率,完成下列问题.
(Ⅰ)将![]() 列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
(Ⅱ)当处罚金额为10元时,行人闯红灯的概率会比不进行处罚降低多少;
(Ⅲ)结合调查结果,谈谈如何治理行人闯红灯现象.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
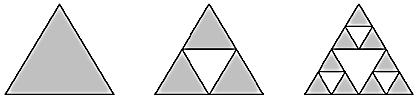
【题目】谢尔宾斯基三角形(Sierpinskitriangle)是由波兰数学家谢尔宾斯基在1915年提出的,如图先作一个三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色三角形代表挖去的面积,那么灰色三角形为剩下的面积(我们称灰色部分为谢尔宾斯基三角形).若通过该种方法把一个三角形挖3次,然后在原三角形内部随机取一点,则该点取自谢尔宾斯基三角形的概率为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在区间
在区间![]() (
(![]() 为自然对数的底数)上有唯一的零点,求实数
为自然对数的底数)上有唯一的零点,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() (
(![]() 为自然对数的底数)上存在一点
为自然对数的底数)上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com