
科目: 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() .直线
.直线![]() 被称作为椭圆
被称作为椭圆![]() 的一条准线.点
的一条准线.点![]() 在椭圆
在椭圆![]() 上(异于椭圆左、右顶点),过点
上(异于椭圆左、右顶点),过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 相切,且与直线
相切,且与直线![]() 相交于点
相交于点![]() .
.
(1)求证:![]() .
.
(2)若点![]() 在
在![]() 轴的上方,
轴的上方,![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年9月26日,携程网发布《2019国庆假期旅游出行趋势预测报告》,2018年国庆假日期间,西安共接待游客1692.56万人次,今年国庆有望超过2000万人次,成为西部省份中接待游客量最多的城市.旅游公司规定:若公司某位导游接待旅客,旅游年总收人不低于40(单位:万元),则称该导游为优秀导游.经验表明,如果公司的优秀导游率越高,则该公司的影响度越高.已知甲、乙两家旅游公司各有导游40名,统计他们一年内旅游总收入,分别得到甲公司的频率分布直方图和乙公司的频数分布表如下:

(1)求![]() 的值,并比较甲、乙两家旅游公司,哪家的影响度高?
的值,并比较甲、乙两家旅游公司,哪家的影响度高?
(2)求甲公司一年内导游旅游总收入的中位数,乙公司一年内导游旅游总收入的平均数.(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正六棱锥![]() 的底面边长为
的底面边长为![]() ,高为
,高为![]() .现从该棱锥的
.现从该棱锥的![]() 个顶点中随机选取
个顶点中随机选取![]() 个点构成三角形,设随机变量
个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为
为等比数列,公比为![]() .令
.令![]() .
.
(1)若![]() .
.
①当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②设![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小?并证明你的结论.
的大小?并证明你的结论.
(2)问集合![]() 中最多有多少个元素?并证明你的结论.
中最多有多少个元素?并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
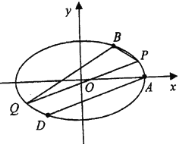
【题目】已知椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆上,点
在椭圆上,点![]() 与点
与点![]() 关于原点对称.
关于原点对称.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求经过点![]() ,
,![]() 且和
且和![]() 轴相切的圆的方程;
轴相切的圆的方程;
(3)若![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]() ,
,![]() 的两个点,且
的两个点,且![]() ,点
,点![]() 在直线
在直线![]() 的上方,试判断
的上方,试判断![]() 的平分线是否经过
的平分线是否经过![]() 轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某景区是一个以![]() 为圆心,半径为
为圆心,半径为![]() 的圆形区域,道路
的圆形区域,道路![]() ,
,![]() 成
成![]() 角,且均和景区边界相切,现要修一条与景区相切的观光木栈道
角,且均和景区边界相切,现要修一条与景区相切的观光木栈道![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上,修建的木栈道
上,修建的木栈道![]() 与道路
与道路![]() ,
,![]() 围成的三角地块
围成的三角地块![]() .
.

(1)求修建的木栈道![]() 与道路
与道路![]() ,
,![]() 围成的三角地块
围成的三角地块![]() 面积的最小值;
面积的最小值;
(2)若景区中心![]() 与木栈道
与木栈道![]() 段连线的
段连线的![]() .
.
①将木栈道![]() 的长度表示为
的长度表示为![]() 的函数,并指定定义域;
的函数,并指定定义域;
②求出木栈道![]() 的长度最小值.
的长度最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com