
科目: 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (k为常数,
(k为常数,![]() 且
且![]() ).
).
(1)在下列条件中选择一个________使数列![]() 是等比数列,说明理由;
是等比数列,说明理由;
①数列![]() 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
②数列![]() 是首项为4,公差为2的等差数列;
是首项为4,公差为2的等差数列;
③数列![]() 是首项为2,公差为2的等差数列的前n项和构成的数列.
是首项为2,公差为2的等差数列的前n项和构成的数列.
(2)在(1)的条件下,当![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
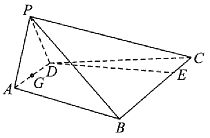
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了调节高三学生学习压力,某校高三年级举行了拔河比赛,在赛前三位老师对前三名进行了预测,于是有了以下对话:老师甲:“7班男生比较壮,7班肯定得第一名”.老师乙:“我觉得14班比15班强,14班名次会比15班靠前”.老师丙:“我觉得7班能赢15班”.最后老师丁去观看完了比赛,回来后说:“确实是这三个班得了前三名,且无并列,但是你们三人中只有一人预测准确”.那么,获得一、二、三名的班级依次为( )
A.7班、14班、15班B.14班、7班、15班
C.14班、15班、7班D.15班、14班、7班
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,对于给定实数
,对于给定实数![]() ,总存在实数
,总存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 恰有3个不同的实数根.
恰有3个不同的实数根.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)记![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,经过点
两点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.
(1)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(2)问是否存在直线![]() ,
,![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
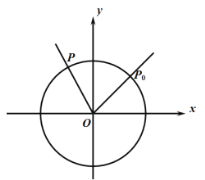
【题目】如图,单位圆上有一点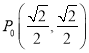 ,点
,点![]() 以点
以点![]() 为起点按逆时针方向以每秒
为起点按逆时针方向以每秒![]() 弧度作圆周运动,点
弧度作圆周运动,点![]() 的纵坐标
的纵坐标![]() 是关于时间
是关于时间![]() 的函数,记作
的函数,记作![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)若将函数![]() 向左平移
向左平移![]() 个单位长度后,得到的曲线关于
个单位长度后,得到的曲线关于![]() 轴对称,求
轴对称,求![]() 的最小正值,并求此时
的最小正值,并求此时![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】设有编号分别为1,2,3,4,5,6,7,8的八个小球和编号为1,2,3,4,5,6,7,8的八个盒子.现将这八个小球随机放入八个盒子内,要求每个盒子内放一个球,要求编号为偶数的小球在编号为偶数的盒子内,且至少有四个小球在相同编号的盒子内,则一共有______种投放方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com