
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于两点
交于两点![]() ,
,![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值.经数据处理后得到该样本的频率分布直方图,其中质量指标值不大于1.50的茎叶图如图所示,以这100件产品的质量指标值在各区间内的频率代替相应区间的概率.
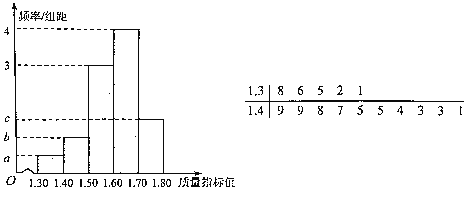
(1)求图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计这种产品质量指标值的平均数及方差(说明:①同一组中的数据用该组区间的中点值作代表;②方差的计算只需列式正确);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于1.50的产品至少要占全部产品的![]() ”的规定?
”的规定?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: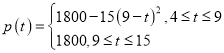 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com