
科目: 来源: 题型:
【题目】已知![]() 是定义在[-1,1]上的奇函数且
是定义在[-1,1]上的奇函数且![]() ,若ab∈[-1,1],a+b≠0,有
,若ab∈[-1,1],a+b≠0,有![]() 成立.
成立.
(1)判断函数![]() 在[-1,1]上是增函数还是减函数,并加以证明.
在[-1,1]上是增函数还是减函数,并加以证明.
(2)解不等式![]() .
.
(3)若对所有![]()
![]() ,
, ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是等比数列,______,
是等比数列,______,![]() ,
,![]() ,
,![]() .是否存在k,使得
.是否存在k,使得![]() 且
且![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,E为
,E为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
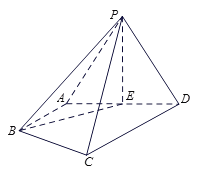
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点M,使得
上是否存在点M,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为2019年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊5个民生项目,得到如下信息:
①若该地区引进甲项目,就必须引进与之配套的乙项目;
②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;
③乙、丙两个项目之间有冲突,两个项目只能引进一个;
④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;
⑤若引进项目戊,甲、丁两个项目也必须引进.
则该地区应引进的项目为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y=f(x),x∈[1,+∞),数列{an}满足![]() ,
,
①函数f(x)是增函数;
②数列{an}是递增数列.
写出一个满足①的函数f(x)的解析式______.
写出一个满足②但不满足①的函数f(x)的解析式______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若满足:对任意
,若满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界
的上界
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否是有界函数,若是,说明理由,并写出
上是否是有界函数,若是,说明理由,并写出![]() 所有上界的值的集合;若不是,也请说明理由.
所有上界的值的集合;若不是,也请说明理由.
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com