
科目: 来源: 题型:
【题目】给出下列四个结论:①若![]() 是真命题,则
是真命题,则![]() 可能是真命题;②命题“若
可能是真命题;②命题“若![]() 则
则![]() ”与命题“若
”与命题“若![]() ,则
,则![]() ”互为逆否命题;③若“
”互为逆否命题;③若“![]() 或
或![]() ”是假命题,则“
”是假命题,则“![]() 且
且![]() ”是真命题;④若
”是真命题;④若![]() 是
是![]() 的充分条件,
的充分条件,![]() 是
是![]() 的充分条件,则
的充分条件,则![]() 是
是![]() 的充分条件.其中正确的个数为( )
的充分条件.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】国庆节期间,滕州市实验小学举行了一次科普知识竞赛活动,设置了一等奖、二等奖、三等奖、四等奖及纪念奖,获奖人数的分配情况如图所示,各个奖品的单价分别为:一等奖50元、二等奖20元、三等奖10元,四等奖5元,纪念奖2元,则以下说法中不正确的是( )
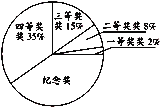
A.获纪念奖的人数最多B.各个奖项中二等奖的总费用最高
C.购买奖品的费用平均数为6.65元D.购买奖品的费用中位数为5元
查看答案和解析>>
科目: 来源: 题型:
【题目】有限个元素组成的集合![]() ,
,![]() ,记集合
,记集合![]() 中的元素个数为
中的元素个数为![]() ,即
,即![]() .定义
.定义![]() ,集合
,集合![]() 中的元素个数记为
中的元素个数记为![]() ,当
,当![]() 时,称集合
时,称集合![]() 具有性质
具有性质![]() .
.
(1)![]() ,
,![]() ,判断集合
,判断集合![]() ,
,![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)设集合![]() ,
,![]() 且
且![]() (
(![]() ),若集合
),若集合![]() 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)设集合![]() ,其中数列
,其中数列![]() 为等比数列,
为等比数列,![]() (
(![]() )且公比为有理数,判断集合
)且公比为有理数,判断集合![]() 是否具有性质
是否具有性质![]() 并说明理由.
并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,离心率为
,离心率为![]() .直线
.直线![]() 过点
过点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若四边形
,若四边形![]() 为平行四边形,求此时直线
为平行四边形,求此时直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年,北京将实行新的高考方案.新方案规定:语文数学和英语是考生的必考科目,考生还需从物理化学生物历史地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定,例如,学生甲选择“物理化学和生物”三个选考科目,则学生甲的选考方案确定,“物理化学和生物”为其选考方案.
某校为了解高一年级840名学生选考科目的意向,随机选取60名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有16人 | 16 | 16 | 8 | 4 | 2 | 2 |
选考方案待确定的有12人 | 8 | 6 | 0 | 2 | 0 | 0 | |
女生 | 选考方案确定的有20人 | 6 | 10 | 20 | 16 | 2 | 6 |
选考方案待确定的有12人 | 2 | 8 | 10 | 0 | 0 | 2 |
(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(2)从选考方案确定的16名男生中随机选出2名,求恰好有一人选“物理化学生物”的概率;
(3)从选考方案确定的16名男生中随机选出2名,设随机变量 ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】长沙市为了支援边远山区的教育事业,组织了一支由13名教师组成的队伍下乡支教,记者采访队长时询问这个团队的构成情况,队长回答:“(1)有中学高级教师;(2)中学教师不多于小学教师;(3)小学高级教师少于中学中级教师;(4)小学中级教师少于小学高级教师;(5)支教队伍的职称只有小学中级、小学高级、中学中级、中学高级;(6)无论是否把我计算在内,以上条件都成立.”由队长的叙述可以推测出他的学段及职称分别是____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项,共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,特招聘了3万名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
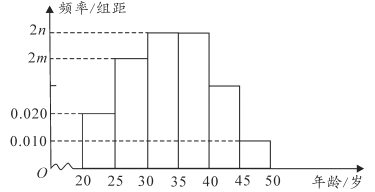
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)本次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: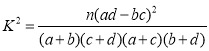 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com