
科目: 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)若以![]() 为直径的圆恰好经过椭圆右焦点
为直径的圆恰好经过椭圆右焦点![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
(2)求证:![]() 的内切圆的圆心在定直线
的内切圆的圆心在定直线![]() 上.
上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() ,
,![]() 在边
在边![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都与平面
都与平面![]() 垂直,如图(2).
垂直,如图(2).
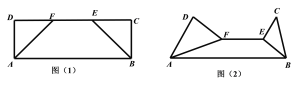
(1)试判断图(2)中直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求平面![]() 和平面
和平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() ,
,![]() ,
,![]() 三个农业扶贫项目进驻某村,对该村仅有的甲、乙、丙、丁四个贫困户进行产业帮扶.经过前期实际调研得知,这四个贫困户选择
三个农业扶贫项目进驻某村,对该村仅有的甲、乙、丙、丁四个贫困户进行产业帮扶.经过前期实际调研得知,这四个贫困户选择![]() ,
,![]() ,
,![]() 三个扶贫项目的意向如下表:
三个扶贫项目的意向如下表:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向项目中随机选取一项,且每个项目至多有两个贫困户选择,则不同的选法种数有( )
A.24种B.16种C.10种D.8种
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
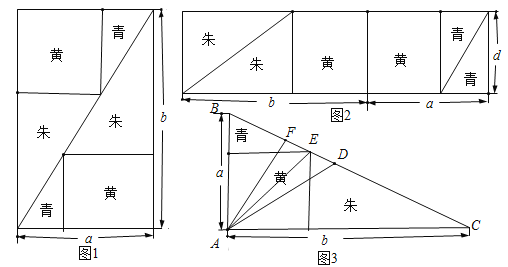
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得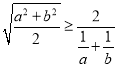 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目: 来源: 题型:
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目: 来源: 题型:
【题目】已知有穷数列A:![]() (
(![]() 且
且![]() ).定义数列A的“伴生数列”B:
).定义数列A的“伴生数列”B:![]() ,其中
,其中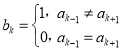 (
(![]() ),规定
),规定![]() ,
,![]() .
.
(1)写出下列数列的“伴生数列”:
①1,2,3,4,5;
②1,![]() ,1,
,1,![]() ,1.
,1.
(2)已知数列B的“伴生数列”C:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,且满足
,且满足![]() (
(![]() ,2,…,n).
,2,…,n).
(i)若数列B中存在相邻两项为1,求证:数列B中的每一项均为1;
(ⅱ)求数列C所有项的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com