
科目: 来源: 题型:
【题目】数![]() (其中
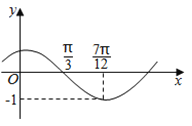
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )
A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,统计他们每天加工的零件数,得到如下数据:

将频率作为概率,解答下列问题:
(1)当![]() 时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
(2)若根据上表得到以下频率分布直方图,估计全体新员工每天加工零件数的平均数为222个,求![]() 的值(每组数据以中点值代替);
的值(每组数据以中点值代替);
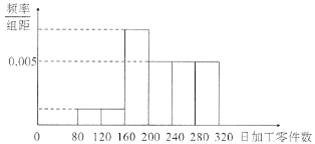
(3)在(2)的条件下,工厂按工作熟练度将新员工分为三个等级:日加工零件数未达200的员工为C级;达到200但未达280的员工为B级;其他员工为A级.工厂打算将样本中的员工编入三个培训班进行全员培训:A,B,C三个等级的员工分别参加高级、中级、初级培训班,预计培训后高级、中级、初级培训班的员工每人的日加工零件数分别可以增加20,30,50.现从样本中随机抽取1人,其培训后日加工零件数增加量为X,求随机变量X的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于
(t为参数),直线l与曲线C分别交于![]() 两点.
两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记![]() 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率![]() 取得最大值的整数
取得最大值的整数![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
科目: 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)烘焙店记录了100天这种蛋糕的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16个这种蛋糕,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列与数学期望及方差;
的分布列与数学期望及方差;
②若烘焙店一天加工16个或17个这种蛋糕,仅从获得利润大的角度考虑,你认为应加工16个还是17个?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com