
科目: 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生55人,求
名学生中含男生55人,求![]() 的值;
的值;
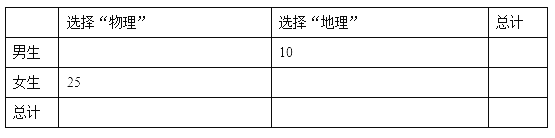
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取到的女生中按(2)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
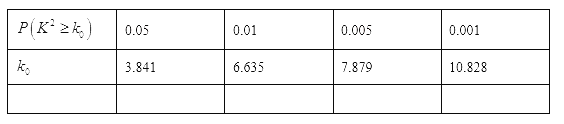
附:![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
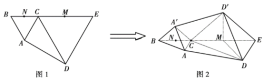
【题目】如图1,平面四边形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]()
![]() 分别是
分别是![]() 和
和![]() 的中点,将四边形
的中点,将四边形![]() 沿
沿![]() 向上翻折至四边形
向上翻折至四边形![]() 的位置,使二面角
的位置,使二面角![]() 为直二面角,如图2所示.
为直二面角,如图2所示.
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:
之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:

其中m,n是正整数.
(Ⅰ)若该校高一年级有280学生,试估计高一年级“体质优秀”的学生人数;
(Ⅱ)若从高一年级抽取的7名学生中随机抽取2人,记X为抽取的2人中为“体质良好”的学生人数,求X的分布列及数学期望;
(Ⅲ)设两个年级被抽取学生的测试成绩的平均数相等,当高二年级被抽取学生的测试成绩的方差最小时,写出m,n的值.(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】某建材商场国庆期间搞促销活动,规定:如果顾客选购物品的总金额不超过600元,则不享受任何折扣优惠;如果顾客选购物品的总金额超过600元,则超过600元部分享受一定的折扣优惠,折扣优惠按下表累计计算.
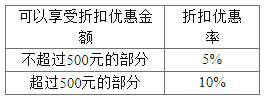
某人在此商场购物获得的折扣优惠金额为30元,则他实际所付金额为____元.
查看答案和解析>>
科目: 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为了调查某款电视机的寿命,研究人员对该款电视机进行了相应的测试,将得到的数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
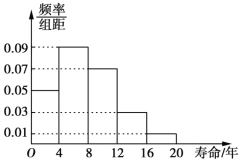
,![]() ,并统计如图所示:
,并统计如图所示:
并对不同性别的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均寿命;
(2)根据表中数据,能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关;
(3)以频率估计概率,若在该款电视机的生产线上随机抽取4台,记其中寿命不低于4年的电视机的台数为X,求X的分布列及数学期望.
参考公式及数据: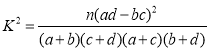 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为正整数,区间
为正整数,区间![]() (其中
(其中![]() ,
,![]() )同时满足下列两个条件:
)同时满足下列两个条件:
①对任意![]() ,存在
,存在![]() 使得
使得![]() ;
;
②对任意![]() ,存在
,存在![]() ,使得
,使得![]() (其中
(其中![]() ).
).
(Ⅰ)判断![]() 能否等于
能否等于![]() 或
或![]() ;(结论不需要证明).
;(结论不需要证明).
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)研究![]() 是否存在最大值,若存在,求出
是否存在最大值,若存在,求出![]() 的最大值;若不在在,说明理由.
的最大值;若不在在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com