【题目】已知函数.

（1）若在上存在极大值，求的取值范围；

（2）若轴是曲线的一条切线，证明：当时，.

【题目】某语文报社为研究学生课外阅读时间与语文考试中的作文分数的关系，随机调查了本市某中学高三文科班名学生每周课外阅读时间（单位：小时）与高三下学期期末考试中语文作文分数，数据如下表：

（1）根据上述数据，求出高三学生语文作文分数与该学生每周课外阅读时间的线性回归方程，并预测某学生每周课外阅读时间为小时时其语文作文成绩；

（2）从这人中任选人，这人中至少有人课外阅读时间不低于小时的概率.

参考公式：，其中，

参考数据：，，

【题目】已知函数（且）.

（1）讨论的单调性；

（2）对任意，恒成立，求的取值范围.

【题目】已知椭圆过点，且其离心率为，过坐标原点作两条互相垂直的射线与椭圆分别相交于，两点.

（1）求椭圆的方程；

（2）是否存在圆心在原点的定圆与直线总相切？若存在，求定圆的方程；若不存在，请说明理由.

（1）若在本次考试中，规定数学在80分以上（包括80分）且物理在75分以上（包括75分）的学生为理科小能手.从这6个学生中抽出2个学生，设表示理科小能手的人数，求的分布列和数学期望；

（2）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系，在上述表格是正确的前提下，用表示数学成绩，用表示物理成绩，求与的回归方程.

参考数据和公式：，其中，.

【题目】已知四棱锥中，底面为直角梯形，平面，且，，.

（1）求证：平面平面；

（2）若与平面所成的角为，求二面角的余弦值.

【题目】在平面直角坐标系中，直线的参数方程为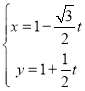(为参数).以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程.

（Ⅰ）求直线的极坐标方程和曲线的直角坐标方程；

（Ⅱ）若直线与曲线交于，两点，求的大小.

【题目】已知函数，曲线在点处的切线方程是.

（Ⅰ）求实数，的值;

（Ⅱ）若函数有两个不同的零点，，求证：.

【题目】如图所示，直三棱柱的底面为等腰直角三角形，其中，点是线段的中点.

（Ⅰ）若点满足，且，求的值；

（Ⅱ）求二面角的余弦值.

【题目】为调查某校学生每周体育锻炼落实的情况，采用分层抽样的方法，收集100位学生每周平均锻炼时间的样本数据(单位:).根据这100个样本数据，制作出学生每周平均锻炼时间的频率分布直方图(如图所示).

（Ⅰ）估计这100名学生每周平均锻炼时间的平均数和样本方差(同一组中的数据用该组区间的中点值作代表)；

（Ⅱ）由频率分布直方图知，该校学生每周平均锻炼时间近似服从正态分布，其中近似为样本平均数，近似为样本方差.

（i）求；

（ii）若该校共有5000名学生，记每周平均锻炼时间在区间的人数为，试求.

附：，若~，，.