
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,且∠AOC=120°,PA⊥平面ABC,AB=4,PA=2![]() ,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
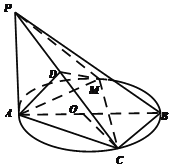
(1)证明:AD⊥PB;
(2)当三棱锥D﹣ACM体积最大时,求面MAD与面MCD所成二面角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如表中数表为“森德拉姆筛”,其特点是每行每列都成等差数列,记第i行,第j列的数为aij,则数字41在表中出现的次数为( )
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
A.4B.8C.9D.12
查看答案和解析>>
科目: 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
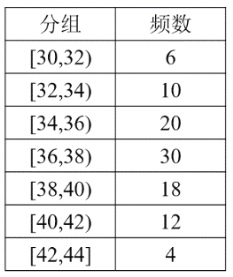
(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
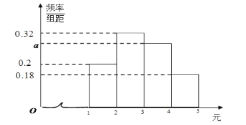
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合A={1,2,3,4}和集合B={1,2,3,…,n},其中n≥5,![]() .从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
.从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
(1)当n=5时,求随机变量X的概率分布和数学期望![]() ;
;
(2)求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD, PA=AD=2,E,F分别为PA,AB的中点,且DF⊥CE.
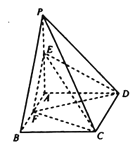
(1)求AB的长;
(2)求直线CF与平面DEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com