
科目: 来源: 题型:
【题目】设抛物线![]() 的方程为
的方程为![]() ,其中常数
,其中常数![]() ,
,![]() 是抛物线
是抛物线![]() 的焦点.
的焦点.
(1)若直线![]() 被抛物线
被抛物线![]() 所截得的弦长为6,求
所截得的弦长为6,求![]() 的值;
的值;
(2)设![]() 是点
是点![]() 关于顶点
关于顶点![]() 的对称点,
的对称点,![]() 是抛物线
是抛物线![]() 上的动点,求
上的动点,求![]() 的最大值;
的最大值;
(3)设![]() ,
,![]() 、
、![]() 是两条互相垂直,且均经过点
是两条互相垂直,且均经过点![]() 的直线,
的直线,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,空间几何体由两部分构成,上部是一个底面半径为1,高为2的圆锥,下部是一个底面半径为1,高为2的圆柱,圆锥和圆柱的轴在同一直线上,圆锥的下底面与圆柱的上底面重合,点![]() 是圆锥的顶点,
是圆锥的顶点,![]() 是圆柱下底面的一条直径,
是圆柱下底面的一条直径,![]() 、
、![]() 是圆柱的两条母线,
是圆柱的两条母线,![]() 是弧
是弧![]() 的中点.
的中点.
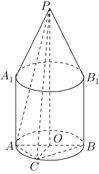
(1)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定数列![]() ,记该数列前
,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,即
,即![]() ,该数列后
,该数列后![]() 项
项![]() 中的最小项为
中的最小项为![]() ,记
,记![]() ,
,![]() ;
;
(1)对于数列:3,4,7,1,求出相应的![]() ,
,![]() ,
,![]() ;
;
(2)若![]() 是数列
是数列![]() 的前
的前![]() 项和,且对任意
项和,且对任意![]() ,有
,有![]() ,其中
,其中![]() 为实数,
为实数,![]() 且
且![]() ,
,![]() .
.
(ⅰ)设![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(ⅱ)若数列![]() 对应的
对应的![]() 满足
满足![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以椭圆![]() (
(![]() )的右焦点
)的右焦点![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() (其中
(其中![]() 为已知椭圆的半焦距),过椭圆上一点
为已知椭圆的半焦距),过椭圆上一点![]() 作此圆的切线,切点为
作此圆的切线,切点为![]() .
.
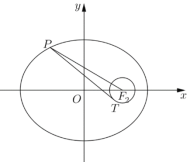
(1)若![]() ,
,![]() 为椭圆的右顶点,求切线长
为椭圆的右顶点,求切线长![]() ;
;
(2)设圆![]() 与
与![]() 轴的右交点为
轴的右交点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,若
两点,若![]() 恒成立,且
恒成立,且![]() .求:
.求:
(ⅰ)![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 被圆
被圆![]() 所截得弦长的最大值.
所截得弦长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业,调整后这
)名员工从事第三产业,调整后这![]() 名员工他们平均每人创造利润为
名员工他们平均每人创造利润为![]() 万元,剩下的员工平均每人每年创造的利润可以提高
万元,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整多少名员工从事第三产业?
(2)设![]() ,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求
,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
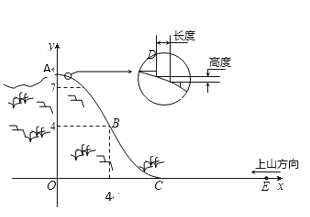
【题目】某旅游胜地欲开发一座景观山,从山的侧面进行勘测,迎面山坡线![]() 由同一平面的两段抛物线组成,其中
由同一平面的两段抛物线组成,其中![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向下,
为顶点、开口向下,![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向上,以过山脚(点
为顶点、开口向上,以过山脚(点![]() )的水平线为
)的水平线为![]() 轴,过山顶(点
轴,过山顶(点![]() )的铅垂线为
)的铅垂线为![]() 轴建立平面直角坐标系如图(单位:百米).已知
轴建立平面直角坐标系如图(单位:百米).已知![]() 所在抛物线的解析式
所在抛物线的解析式![]() ,
,![]() 所在抛物线的解析式为
所在抛物线的解析式为![]()
(1)求![]() 值,并写出山坡线
值,并写出山坡线![]() 的函数解析式;
的函数解析式;
(2)在山坡上的700米高度(点![]() )处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点
)处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点![]() 处,
处,![]() (米),假设索道
(米),假设索道![]() 可近似地看成一段以
可近似地看成一段以![]() 为顶点、开口向上的抛物线
为顶点、开口向上的抛物线![]() 当索道在
当索道在![]() 上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
(3)为了便于旅游观景,拟从山顶开始、沿迎面山坡往山下铺设观景台阶,台阶每级的高度为20厘米,长度因坡度的大小而定,但不得少于20厘米,每级台阶的两端点在坡面上(见图).试求出前三级台阶的长度(精确到厘米),并判断这种台阶能否一直铺到山脚,简述理由?
查看答案和解析>>
科目: 来源: 题型:
【题目】若正项数列![]() 满足:
满足:![]() ,则称此数列为“比差等数列”.
,则称此数列为“比差等数列”.
(1)试写出一个“比差等数列”的前![]() 项;
项;
(2)设数列![]() 是一个“比差等数列”,问
是一个“比差等数列”,问![]() 是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
(3)已知数列![]() 是一个“比差等数列”,
是一个“比差等数列”,![]() 为其前
为其前![]() 项的和,试证明:
项的和,试证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】若存在![]() 与正实数
与正实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在
在![]() 处存在距离为
处存在距离为![]() 的对称点,把具有这一性质的函数
的对称点,把具有这一性质的函数![]() 称之为“
称之为“![]() 型函数”.
型函数”.
(1)设![]() ,试问
,试问![]() 是否是“
是否是“![]() 型函数”?若是,求出实数
型函数”?若是,求出实数![]() 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)设![]() 对于任意
对于任意![]() 都是“
都是“![]() 型函数”,求实数
型函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com