
科目: 来源: 题型:
【题目】《上海市生活垃圾管理条例》于2019年7月1日正式实施,某小区全面实施垃圾分类处理,已知该小区每月垃圾分类处理量不超过300吨,每月垃圾分类处理成本![]() (元)与每月分类处理量
(元)与每月分类处理量![]() (吨)之间的函数关系式可近似表示为
(吨)之间的函数关系式可近似表示为![]() ,而分类处理一吨垃圾小区也可以获得300元的收益.
,而分类处理一吨垃圾小区也可以获得300元的收益.
(1)该小区每月分类处理多少吨垃圾,才能使得每吨垃圾分类处理的平均成本最低;
(2)要保证该小区每月的垃圾分类处理不亏损,每月的垃圾分类处理量应控制在什么范围?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于曲线![]() 所在的平面上的定点
所在的平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线
对于曲线![]() 上的任意两个不同的点
上的任意两个不同的点![]() 恒成立,则称角
恒成立,则称角![]() 为曲线
为曲线![]() 的“
的“![]() 点视角”,并称其中最小的“
点视角”,并称其中最小的“![]() 点视角”为曲线
点视角”为曲线![]() 相对于点
相对于点![]() 的”
的”![]() 点确视角”.已知曲线
点确视角”.已知曲线![]() 和圆
和圆![]() 是
是![]() 轴上一点
轴上一点
(1)对于坐标原点![]() ,写出曲线
,写出曲线![]() 的“
的“![]() 点确视角”的大小;
点确视角”的大小;
(2)若![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值;
的最小值;
(3)若曲线![]() 和圆
和圆![]() 的“
的“![]() 点确视角”相等,求
点确视角”相等,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一列函数![]() ,设直线
,设直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的最小值,并指出此时
的最小值,并指出此时![]() 的取值;
的取值;
(2)在![]() 中任取一个函数,求该函数在
中任取一个函数,求该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率;
上是减函数的概率;
(3)是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
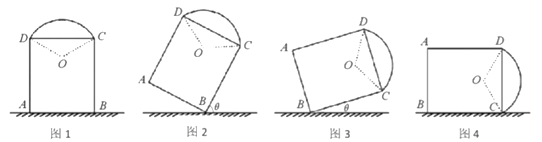
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() 的长分别为
的长分别为![]() 米和
米和![]() 米,上部是圆心为
米,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]()
(1)求图1中拱门最高点到地面的距离:
(2)现欲以![]() 点为支点将拱门放倒,放倒过程中矩形
点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示,设
所在的平面始终与地面垂直,如图2、图3、图4所示,设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .若拱门上的点到地面的最大距离恰好为
.若拱门上的点到地面的最大距离恰好为![]() 到地面的距离,试求
到地面的距离,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() .
.
(1)求以![]() 为焦点,原点为顶点的抛物线方程;
为焦点,原点为顶点的抛物线方程;
(2)若椭圆![]() 上点
上点![]() 满足
满足![]() ,求
,求![]() 的纵坐标
的纵坐标![]() ;
;
(3)设![]() ,若椭圆
,若椭圆![]() 上存在两个不同点
上存在两个不同点![]() 、
、![]() 满足
满足![]() ,证明:直线
,证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com