
科目: 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为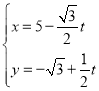 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.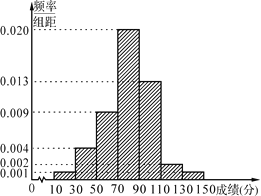
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点O为极点,以x轴的正半轴为极轴建立极坐标系.
为参数),以坐标原点O为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)射线l的极坐标方程为![]() ,若l分别与
,若l分别与![]() ,
,![]() 交于异于极点的
交于异于极点的![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
(1)求甲恰有2个题目答对的概率;
(2)求乙答对的题目数X的分布列;
(3)试比较甲,乙两人平均答对的题目数的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
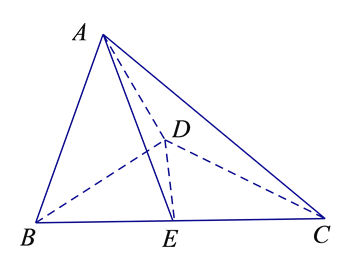
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=2,直线CA与平面ABD所成角的正弦值为![]() ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 是三条不同的直线,
是三条不同的直线,![]() 、
、![]() 、
、![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确命题的序号是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,青蒿素作为一线抗疟药品得到大力推广某农科所为了深入研究海拔因素对青蒿素产量的影响,在山上和山下的试验田中分别种植了![]() 株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了
株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了![]() 株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
编号位置 | ① | ② | ③ | ④ |
山上 |
|
|
|
|
山下 |
|
|
|
|
(1)根据样本数据,试估计山下试验田青蒿素的总产量;
(2)记山上与山下两块试验田单株青蒿素产量的方差分别为![]() ,
,![]() ,根据样本数据,试估计
,根据样本数据,试估计![]() 与
与![]() 的大小关系(只需写出结论);
的大小关系(只需写出结论);
(3)从样本中的山上与山下青蒿中各随机选取![]() 株,记这
株,记这![]() 株的产量总和为
株的产量总和为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com