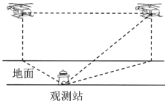
【题目】2019年10月1日，在庆祝新中国成立70周年阅兵中，由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门，壮军威，振民心，令世人瞩目．飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析．一次飞行训练中，地面观测站观测到一架参阅直升飞机以千米/小时的速度在同一高度向正东飞行，如图，第一次观测到该飞机在北偏西的方向上，1分钟后第二次观测到该飞机在北偏东的方向上，仰角为，则直升机飞行的高度为________千米．（结果保留根号）

【题目】某数学小组到进行社会实践调查，了解到某公司为了实现1000万元利润目标，准备制定激励销售人员的奖励方案：在销售利润超过10万元时，按销售利润进行奖励，且奖金y（单位：万元）随销售利润x（单位：万元）的增加而增加，但奖金总数不超过5万元，同时奖金不超过利润的25%．同学们利用函数知识，设计了如下的函数模型，其中符合公司要求的是（参考数据：，）( )

A.B.C.D.

【题目】设函数的定义城为D，若满足条件：存在，使在上的值城为（且），则称为“k倍函数”，给出下列结论：①是“1倍函数”；②是“2倍函数”：③是“3倍函数”．其中正确的是（ ）

A.①②B.①③C.②③D.①②③

【题目】已知椭圆的一个焦点与抛物线的焦点重合，且椭圆的离心率为.

（1）求椭圆的标准方程；

（2）直线交椭圆于、两点，线段的中点为，直线是线段的垂直平分线，求证：直线过定点，并求出该定点的坐标．

【题目】设函数为常数．

（1）当时，求函数的图象在点处的切线方程；

（2）若函数有两个不同的零点，，

①当时，求的最小值；

②当时，求的值．

【题目】在数列的每相邻两项之间插入此两项的和，形成新的数列，这样的操作叫做该数列的一次拓展．如数列1，2，经过第1次拓展得到数列1，3，2；经过第2次拓展得到数列1，4，3，5，2；设数列a，b，c经过第n次拓展后所得数列的项数记为，所有项的和记为．

（1）求，，；

（2）若，求n的最小值；

（3）是否存在实数a，b，c，使得数列为等比数列，若存在，求a，b，c满足的条件；若不存在，请说明理由．

【题目】在平面直角坐标系中，已知曲线的参数方程为（为参数），以坐标原点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）设点分别为曲线与曲线上的任意一点，求的最大值；

（2）设直线（为参数）与曲线交于两点，且，求直线的普通方程.

（1）若英语等级考试成绩有一次为优，即可达到某211院校的录取要求.假设某个学生参加每次等级考试事件是独立的，且该生英语等级考试成绩为优的概率都是，求该生在高二上学期的英语等级考试成绩才为优的概率；

（2）据预测，要想报考该211院校的相关院系，省会考的成绩至少在90分以上，才有可能被该校录取.假设该生在省会考六科的成绩，考到90分以上概率都是，设该生在省会考时考到90分以上的科目数为，求的分布列及数学期望.

【题目】如图，四棱锥，，，，为等边三角形，平面平面，为中点.

（1）求证：平面；

（2）求二面角的余弦值.

【题目】已知椭圆中心在原点，焦点在坐标轴上，直线与椭圆在第一象限内的交点是，点在轴上的射影恰好是椭圆的右焦点，椭圆另一个焦点是，且.

（1）求椭圆的方程；

（2）直线过点，且与椭圆交于两点，求的内切圆面积的最大值.