
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数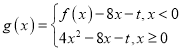 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量![]() (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级![]() 之间的关系为
之间的关系为![]() .
.
(1)已知地震等级划分为里氏![]() 级,根据等级范围又分为三种类型,其中小于
级,根据等级范围又分为三种类型,其中小于![]() 级的为“小地震”,介于
级的为“小地震”,介于![]() 级到
级到![]() 级之间的为“有感地震”,大于
级之间的为“有感地震”,大于![]() 级的为“破坏性地震”若某次地震释放能量约
级的为“破坏性地震”若某次地震释放能量约![]() 焦耳,试确定该次地震的类型;
焦耳,试确定该次地震的类型;
(2)2008年汶川地震为里氏![]() 级,2011年日本地震为里氏
级,2011年日本地震为里氏![]() 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取
级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】将曲线![]() 上每个点的横坐标伸长为原来的
上每个点的横坐标伸长为原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
B.![]() 在
在![]() 上的值域为
上的值域为![]()
C.![]() 的图象关于点
的图象关于点![]() 对称
对称
D.![]() 的图象可由
的图象可由![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
科目: 来源: 题型:
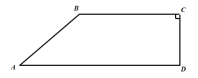
【题目】如图,某山地车训练中心有一直角梯形森林区域![]() ,其四条边均为道路,其中
,其四条边均为道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从
千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从![]() 地出发匀速前往
地出发匀速前往![]() 地,其中甲的行驶路线是
地,其中甲的行驶路线是![]() ,速度为
,速度为![]() 千米/小时,乙的行驶路线是
千米/小时,乙的行驶路线是![]() ,速度为
,速度为![]() 千米/小时.
千米/小时.
(1)若甲、乙两名特训队员到达![]() 地的时间相差不超过
地的时间相差不超过![]() 分钟,求乙的速度
分钟,求乙的速度![]() 的取值范围;
的取值范围;
(2)已知甲、乙两名特训队员携带的无线通讯设备有效联系的最大距离是![]() 千米.若乙先于甲到达
千米.若乙先于甲到达![]() 地,且乙从
地,且乙从![]() 地到
地到![]() 地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度
地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有人玩掷均匀硬币走跳棋的游戏,棋盘上标有第0站(出发地),在第1站,第2站,……,第100站. 一枚棋子开始在出发地,棋手每掷一次硬币,这枚棋子向前跳动一次,若掷出正向,棋子向前跳一站,若掷出反面,棋子向前跳两站,直到棋子跳到第99站(失败收容地)或跳到第100站(胜利大本营),该游戏结束. 设棋子跳到第![]() 站的概率为
站的概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)写出![]() 与
与![]() 、
、![]() 的递推关系
的递推关系![]() );
);
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学研究曲线![]() 的性质,得到如下结论:①
的性质,得到如下结论:①![]() 的取值范围是
的取值范围是![]() ;②曲线
;②曲线![]() 是轴对称图形;③曲线
是轴对称图形;③曲线![]() 上的点到坐标原点的距离的最小值为
上的点到坐标原点的距离的最小值为![]() . 其中正确的结论序号为( )
. 其中正确的结论序号为( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com