
科目: 来源: 题型:
【题目】已知椭圆![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 为等边三角形,过点
为等边三角形,过点![]() 的直线与椭圆
的直线与椭圆![]() 在
在![]() 轴右侧的部分交于
轴右侧的部分交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.

(1)求椭圆的标准方程;
(2)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: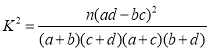 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生,新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通过估算,试判断男、女哪种性别的学生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握认为,愿意参加新生接待工作与性别有关?
附: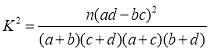 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古典乐器一般按“八音”分类.“八音”是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼·春官·大师》,分为“金、石、土、革、丝、木、匏(páo)、竹”八音.其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器,现从打击乐器、弹拨乐器中任取不同的‘两音’,含有弹拨乐器的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() .(
.(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标和 l的直角坐标方程;
的直角坐标和 l的直角坐标方程;
(2)把曲线![]() 上各点的横坐标伸长为原来的
上各点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,
,![]() 为
为![]() 上动点,求
上动点,求![]() 中点
中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市旅游局为尽快恢复受疫情影响的旅游业,准备在本市的景区推出旅游一卡通(年卡).为了更科学的制定一卡通的有关条例,市旅游局随机调查了2019年到本市景区旅游的1000个游客的年旅游消费支出(单位:百元),并制成如下频率分布直方图:
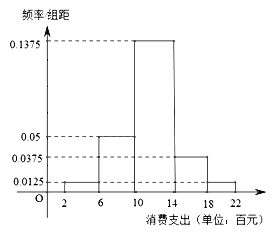
由频率分布直方图,可近似地认为到本市景区旅游的游客,其旅游消费支出服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (同一组数据用该组区间的中点值作代表).
(同一组数据用该组区间的中点值作代表).
(1) 若2019年到本市景区旅游游客为500万人,试估计2019年有多少游客在本市的年旅游消费支出不低于1820元;
(2) 现依次抽取![]() 个游客,假设每个游客的旅游消费支出相互独立,记事件
个游客,假设每个游客的旅游消费支出相互独立,记事件![]() 表示“连续3人的旅游消费支出超出
表示“连续3人的旅游消费支出超出![]() ”.若
”.若![]() 表示
表示![]() 的概率,
的概率,![]() 为常数),且
为常数),且![]() .
.
(ⅰ)求![]() ,
,![]() 及
及![]() ,
,![]() ;
;
(ⅱ)判断并证明数列![]() 从第三项起的单调性,试用概率统计知识解释其实际意义.
从第三项起的单调性,试用概率统计知识解释其实际意义.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆的左右焦点,点
分别为椭圆的左右焦点,点![]() 为椭圆
为椭圆![]() 上的一动点,
上的一动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,点
,点![]() ,证明:直线
,证明:直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com