
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
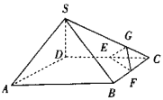
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.2019年6月25日,生活垃圾分类制度入法.到2020年底,先行先试的46个重点城市,要基本建成垃圾分类处理系统;其他地级城市实现公共机构生活垃圾分类全覆盖.某机构欲组建一个有关“垃圾分类”相关事宜的项目组,对各个地区“垃圾分类”的处理模式进行相关报道.该机构从600名员工中进行筛选,筛选方法:每位员工测试![]() ,
,![]() ,
,![]() 三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试
三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试![]() ,
,![]() 两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试
两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试![]() ,
,![]() ,
,![]() 三项工作相互独立,每一项测试“不合格”的概率均为
三项工作相互独立,每一项测试“不合格”的概率均为![]() .
.
(1)记某位员工被认定为“暂定”的概率为![]() ,求
,求![]() ;
;
(2)每位员工不需要重新测试的费用为90元,需要重新测试的总费用为150元,除测试费用外,其他费用总计为1万元,若该机构的预算为8万元,且该600名员工全部参与测试,问上述方案是否会超过预算?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,点
上一点,点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 的另一个交点为
的另一个交点为![]() ,曲线
,曲线![]() 在点
在点![]() 与点
与点![]() 处的切线分别为
处的切线分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 为等边三角形,过点
为等边三角形,过点![]() 的直线与椭圆
的直线与椭圆![]() 在
在![]() 轴右侧的部分交于
轴右侧的部分交于![]() 、
、![]() 两点.
两点.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: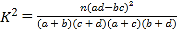 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 的普通方程为
的普通方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,记点
变化时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() . 在以原点
. 在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,若直线
上,若直线![]() 与
与![]() 的夹角为
的夹角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com