【题目】已知函数．

(1)求函数的单调区间及极值；

(2)设时，存在，使方程成立，求实数的最小值．

（1）求顾客抽奖1次能获奖的概率；

（2）若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为，求的分布列和数学期望.

【题目】如图所示，四棱锥中，侧面底面，底面是平行四边形，，，，是中点，点在线段上.

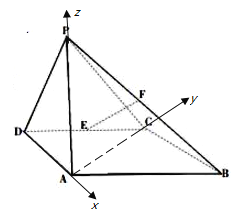
（Ⅰ）证明：；

（Ⅱ）若 ，求实数使直线与平面所成角和直线与平面所成角相等.

【题目】已知抛物线的焦点为，准线为，是上一点，直线与抛物线交于，两点，若，则=

A.B.

C.D.

【题目】某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量（单位：厘米），左图为选取的15名志愿者身高与臂展的折线图，右图为身高与臂展所对应的散点图，并求得其回归方程为，以下结论中不正确的为

A. 15名志愿者身高的极差小于臂展的极差

B. 15名志愿者身高和臂展成正相关关系，

C. 可估计身高为190厘米的人臂展大约为189.65厘米，

D. 身高相差10厘米的两人臂展都相差11.6厘米，

【题目】如图，在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，极坐标系中，弧所在圆的圆心分别为，曲线是弧，曲线是弧，曲线是弧，曲线是弧.

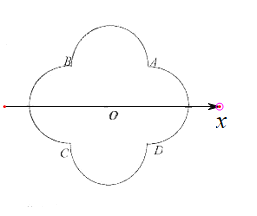
（1）分别写出的极坐标方程；

（2）直线的参数方程为（为参数），点的直角坐标为，若直线与曲线有两个不同交点，求实数的取值范围，并求出的取值范围.

在平面直角坐标系xOy中，点B与点A（-1,1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于.

(Ⅰ)求动点P的轨迹方程；

(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由．

(1)应从该学院三个专业的毕业生中分别抽取多少人？

(2)国家鼓励大学生自主创业，在抽取的18人中，含有“自主创业”就业意向的有6人，且就业意向至少有三个行业的学生有7人.为方便统计，将至少有三个行业就业意向的这7名学生分别记为，，，，，，，统计如下表：

其中“〇”表示有该行业就业意向，“×”表示无该行业就业意向．

①试估计该学院2020届毕业生中有自主创业意向的学生人数；

②现从，，，，，，这7人中随机抽取2人接受采访，设为事件“抽取的2人中至少有一人有自主创业意向”，求事件发生的概率.

【题目】已知函数的导函数为，且对任意的实数x都有（e是自然对数的底数），且，若关于x的不等式的解集中恰有两个整数，则实数m的取值范围是（ ）

A. B. C. D.

【题目】2019年末，武汉出现新型冠状病毒肺炎（）疫情，并快速席卷我国其他地区，传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株，所以目前没有特异治疗方法，防控难度很大.武汉市出现疫情最早，感染人员最多，防控压力最大，武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员，强化网格化管理，不落一户、不漏一人.在排查期间，一户6口之家被确认为“与确诊患者的密切接触者”，这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测，若出现阳性，则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为（）且相互独立，该家庭至少检测了5个人才能确定为“感染高危户”的概率为，当时，最大，则（ ）

A.B.C.D.