
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为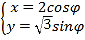 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 轴上方的点
轴上方的点![]() 在抛物线上,且
在抛物线上,且![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 与
与![]() 不重合),设直线
不重合),设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)当![]() 时,求证:直线
时,求证:直线![]() 恒过定点并求出该定点的坐标.
恒过定点并求出该定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
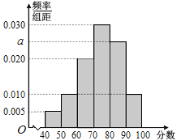
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位为了更好地应对新型冠状病毒肺炎疫情,对单位的职工进行防疫知识培训,所有职工选择网络在线培训和线下培训中的一种方案进行培训.随机抽取了140人的培训成绩,统计发现样本中40个成绩来自线下培训职工,其余来自在线培训的职工,并得到如下统计图表:

(1)写出线下培训茎叶图中成绩的中位数,估算在线培训直方图的中位数(保留一位小数);
(2)得分90分及以上为成绩优秀,完成下边列联表,并判断是否有![]() 的把握认为成绩优秀与培训方式有关?
的把握认为成绩优秀与培训方式有关?
优秀 | 非优秀 | 合计 | |
线下培训 | |||
在线培训 | |||
合计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)试讨论函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,且
,且![]() 恒成立,求a的最大值.
恒成立,求a的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.588 | 2.303 |
查看答案和解析>>
科目: 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com