
科目: 来源: 题型:
【题目】2019新型冠状病毒(2019―nCoV)于2020年1月12日被世界卫生组织命名.冠状病毒是一个大型病毒家族,可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.某医院对病患及家属是否带口罩进行了调查,统计人数得到如下列联表:
戴口罩 | 未戴口罩 | 总计 | |
未感染 | 30 | 10 | 40 |
感染 | 4 | 6 | 10 |
总计 | 34 | 16 | 50 |
(1)根据上表,判断是否有95%的把握认为未感染与戴口罩有关;
(2)从上述感染者中随机抽取3人,记未戴口罩的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: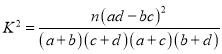 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为A,B,C,D,E五个等级.某试点高中2019年参加“选择考”总人数是2017年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2017年和2019年“选择考”成绩等级结果,得到如图表:


针对该校“选择考”情况,2019年与2017年比较,下列说法正确的是( )
A.获得A等级的人数不变B.获得B等级的人数增加了1倍
C.获得C等级的人数减少了D.获得E等级的人数不变
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司有l000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族”,计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(Ⅰ)完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该公司员工属于“追光族”与“性别”有关;
的把握认为该公司员工属于“追光族”与“性别”有关;
属于“追光族” | 属于“观望者” | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(Ⅱ)已知被抽取的这l00名员工中有6名是人事部的员工,这6名中有3名属于“追光族”现从这6名中随机抽取3名,求抽取到的3名中恰有1名属于“追光族”的概率.
附: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,直线
,直线![]() 过
过![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.![]() 到准线的距离之和最小为8.
到准线的距离之和最小为8.
(1)求抛物线方程;
(2)若抛物线上一点![]() 纵坐标为
纵坐标为![]() ,直线
,直线![]() 分别交准线于
分别交准线于![]() .求证:以
.求证:以![]() 为直径的圆过焦点
为直径的圆过焦点![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数y | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染人数的变化趋势,小王同学打算从①![]() ,②
,②![]() 中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得
中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
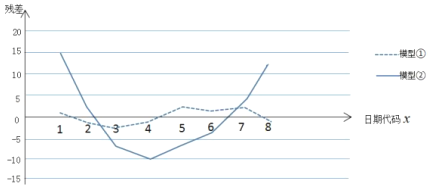
(1)请根据散点图,比较模型①,②的拟合效果,小王应该选择哪个模型?
(2)根据(1)问选定的模型求出相应的回归方程(系数均保留一位小数);
(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数作出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少.
附:回归直线的最小二乘估计参考公式为: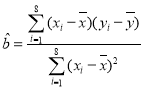 ,
,
查看答案和解析>>
科目: 来源: 题型:
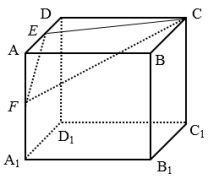
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则以下说法错误的是( )
的中点,则以下说法错误的是( )
A.平面![]() 截正方体所的截面周长为
截正方体所的截面周长为![]()
B.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
C.三棱锥![]() 和
和![]() 体积相等
体积相等
D.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com