
科目: 来源: 题型:
【题目】甲、乙两位同学各有![]() 张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到
张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到![]() 次,或在此之前某入赢得对方所有卡片时,游戏终止.
次,或在此之前某入赢得对方所有卡片时,游戏终止.
(1)设![]() 表示游戏终止时投掷的次数,求
表示游戏终止时投掷的次数,求![]() 的分布列及期望;
的分布列及期望;
(2)求在投掷![]() 次游戏才结束的条件下,甲、乙没有分出胜负的概率.
次游戏才结束的条件下,甲、乙没有分出胜负的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在矩形ABCD中,AB=5,AD=2,点E在线段AB上,且BE=1,将△ADE沿DE折起到A1DE的位置,使得平面A1DE⊥平面BCDE.
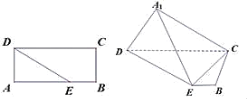
(1)求证:CE⊥平面A1DE;
(2)线段A1C上是否存在一点F,使得BF//平面A1DE?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系内,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 和直线
和直线![]() 化为直角坐标方程;
化为直角坐标方程;
(2)过原点![]() 引一条射线分别交曲线
引一条射线分别交曲线![]() 和直线
和直线![]() 于
于![]() ,
,![]() 两点,射线上另有一点
两点,射线上另有一点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程(写成直角坐标形式的普通方程).
的轨迹方程(写成直角坐标形式的普通方程).
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年12月1日起郑州市施行《郑州市城市生活垃圾分类管理办法》,郑州将正式进入城市生活垃圾分类时代.为了增强社区居民对垃圾分类知识的了解,积极参与到垃圾分类的行动中,某社区采用线下和线上相结合的方式开展了一次200名辖区成员参加的“垃圾分类有关知识”专题培训.为了了解参训成员对于线上培训、线下培训的满意程度,社区居委会随机选取了40名辖区成员,将他们分成两组,每组20人,分别对线上、线下两种培训进行满意度测评,根据辖区成员的评分(满分100分)绘制了如图所示的茎叶图.
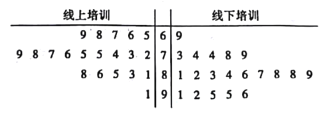
(1)根据茎叶图判断辖区成员对于线上、线下哪种培训的满意度更高,并说明理由.
(2)求这40名辖区成员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”“非常满意”两个等级.
分别视为“基本满意”“非常满意”两个等级.
(ⅰ)利用样本估计总体的思想,估算本次培训共有多少辖区成员对线上培训非常满意;
(ⅱ)根据茎叶图填写下面的列联表.
基本满意 | 非常满意 | 总计 | |
线上培训 | |||
线下培训 | |||
总计 |
并根据列联表判断能否有99.5%的把握认为辖区成员对两种培训方式的满意度有差异?
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7 | 10.828 |
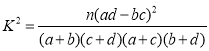 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com