
科目: 来源: 题型:
【题目】某省2020年高考将实施新的高考改革方案.考生的高考总成绩由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、政治、历史、地理6科中选择3门作为选考科目,语文、数学、外语三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科
等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为
等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为![]() ,
,![]() ,求得
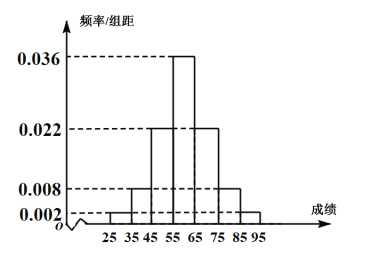
,求得![]() .四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩
.四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩![]() 服从正态分布
服从正态分布![]() ,用这2000名学生的平均物理成绩
,用这2000名学生的平均物理成绩![]() 作为
作为![]() 的估计值,用这2000名学生的物理成绩的方差
的估计值,用这2000名学生的物理成绩的方差![]() 作为
作为![]() 的估计值.
的估计值.
(1)若张明同学在这次考试中的物理原始分为86分,等级为![]() ,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记
,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记![]() 表示这100人中等级成绩在区间
表示这100人中等级成绩在区间![]() 内的人数,求
内的人数,求![]() 最有可能的取值(概率最大);
最有可能的取值(概率最大);
(2)①求![]() ,
,![]() (同一组中的数据用该组区间的中点作代表);
(同一组中的数据用该组区间的中点作代表);
②由①中的数据,记该校高一学生的物理原始分高于84分的人数为![]() ,求
,求![]() .
.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() 是
是![]() 与
与![]() 的等差中项;②
的等差中项;②![]() 是
是![]() 与
与![]() 的等比中项;③数列
的等比中项;③数列![]() 的前5项和为65这三个条件中任选一个,补充在横线中,并解答下面的问题.
的前5项和为65这三个条件中任选一个,补充在横线中,并解答下面的问题.
已知![]() 是公差为2的等差数列,其前
是公差为2的等差数列,其前![]() 项和为
项和为![]() ,________________________.
,________________________.
(1)求![]() ;
;
(2)设![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2013年5月,华人数学家张益唐的论文《素数间的有界距离》在《数学年刊》上发表,破解了困扰数学界长达一个多世纪的难题,证明了孪生素数猜想的弱化形式,即发现存在无穷多差小于7000万的素数对.这是第一次有人证明存在无穷多组间距小于定值的素数对.孪生素数猜想是希尔伯特在1900年提出的23个问题中的第8个,可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,素数对
是素数,素数对![]() 称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() ,其前
,其前![]() 项和为
项和为![]() ,设
,设![]() .
.
(1)若![]() ,
,![]() ,且数列
,且数列![]() 是公差为
是公差为![]() 的等差数列,求
的等差数列,求![]() ;
;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②若对![]() ,且
,且![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 分别为椭圆
分别为椭圆![]() 的左右顶点和右焦点,过点
的左右顶点和右焦点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
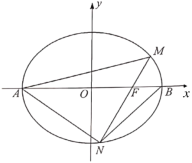
(1)若![]() ,点
,点![]() 与椭圆
与椭圆![]() 左准线的距离为
左准线的距离为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 的斜率是直线
的斜率是直线![]() 斜率的
斜率的![]() 倍.
倍.
①求椭圆![]() 的离心率;
的离心率;
②若椭圆![]() 的焦距为
的焦距为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一块以点![]() 为圆心,半径为
为圆心,半径为![]() 百米的圆形草坪,草坪内距离
百米的圆形草坪,草坪内距离![]() 点
点![]() 百米的
百米的![]() 点有一用于灌溉的水笼头,现准备过点
点有一用于灌溉的水笼头,现准备过点![]() 修一条笔直小路交草坪圆周于
修一条笔直小路交草坪圆周于![]() 两点,为了方便居民散步,同时修建小路
两点,为了方便居民散步,同时修建小路![]() ,其中小路的宽度忽略不计.
,其中小路的宽度忽略不计.
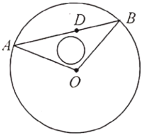
(1)若要使修建的小路的费用最省,试求小路的最短长度;
(2)若要在![]() 区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和
区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com