
科目: 来源: 题型:
【题目】某服装店每年春季以每件15元的价格购入![]() 型号童裤若干,并开始以每件30元的价格出售,若前2个月内所购进的
型号童裤若干,并开始以每件30元的价格出售,若前2个月内所购进的![]() 型号童裤没有售完,则服装店对没卖出的
型号童裤没有售完,则服装店对没卖出的![]() 型号童裤将以每件10元的价格低价处理(根据经验,1个月内完全能够把
型号童裤将以每件10元的价格低价处理(根据经验,1个月内完全能够把![]() 型号童裤低价处理完毕,且处理完毕后,该季度不再购进
型号童裤低价处理完毕,且处理完毕后,该季度不再购进![]() 型号童裤).该服装店统计了过去18年中每年该季度
型号童裤).该服装店统计了过去18年中每年该季度![]() 型号童裤在前2个月内的销售量,制成如下表格(注:视频率为概率).
型号童裤在前2个月内的销售量,制成如下表格(注:视频率为概率).
前2月内的销售量(单位:件) | 30 | 40 | 50 |
频数(单位:年) | 6 | 8 | 4 |
(1)若今年该季度服装店购进![]() 型号童裤40件,依据统计的需求量试求服装店该季度销售
型号童裤40件,依据统计的需求量试求服装店该季度销售![]() 型号童裤获取利润
型号童裤获取利润![]() 的分布列和期望;(结果保留一位小数)
的分布列和期望;(结果保留一位小数)
(2)依据统计的需求量求服装店每年该季度在购进多少件![]() 型号童裤时所获得的平均利润最大.
型号童裤时所获得的平均利润最大.
查看答案和解析>>
科目: 来源: 题型:
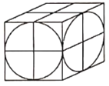
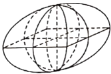
【题目】魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”(如图所示),刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为![]() .若“牟合方盖”的体积为
.若“牟合方盖”的体积为![]() ,则正方体的外接球的表面积为__________.
,则正方体的外接球的表面积为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校周五的课程表设计中,要求安排8节课(上午4节下午4节),分别安排语文数学英语物理化学生物政治历史各一节,其中生物只能安排在第一节或最后一节,数学和英语在安排时必须相邻(注:上午的最后一节与下午的第一节不记作相邻),则周五的课程顺序的编排方法共有( ).
A.4800种B.2400种C.1200种D.240种
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 过抛物线
过抛物线![]() 的焦点,且与该抛物线交于
的焦点,且与该抛物线交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的长是16,
的长是16,![]() 的中点到
的中点到![]() 轴的距离是6,
轴的距离是6,![]() 是坐标原点,则( ).
是坐标原点,则( ).
A.抛物线![]() 的方程是
的方程是![]() B.抛物线的准线方程是
B.抛物线的准线方程是![]()
C.直线![]() 的方程是
的方程是![]() D.
D.![]() 的面积是
的面积是![]()
查看答案和解析>>
科目: 来源: 题型:
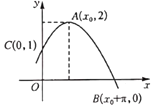
【题目】已知函数![]() 的部分图象如图所示,若将函数
的部分图象如图所示,若将函数![]() 的图象纵坐标不变,横坐标缩短到原来的
的图象纵坐标不变,横坐标缩短到原来的![]() ,再向右平移
,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列命题正确的是( ).
的图象,则下列命题正确的是( ).
A.函数![]() 的解析式为
的解析式为![]()
B.函数![]() 的解析式为
的解析式为![]()
C.函数![]() 图象的一条对称轴是直线
图象的一条对称轴是直线![]()
D.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目: 来源: 题型:
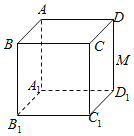
【题目】如图,![]() 是正方体
是正方体![]() 的棱
的棱![]() 的中点,下列命题中真命题是( )
的中点,下列命题中真命题是( )
A.过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]()
![]() 都相交
都相交
B.过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]()
![]() 都垂直
都垂直
C.过![]() 点有且只有一个平面与直线
点有且只有一个平面与直线![]()
![]() 都相交
都相交
D.过![]() 点有且只有一个平面与直线
点有且只有一个平面与直线![]()
![]() 都平行
都平行
查看答案和解析>>
科目: 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学跑步骑行交友及健身饮食指导装备购买等--站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程不仅如此,它还可以根据不同人的体质,制定不同的健身计划小吴根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图根据该折线图,下列结论正确的是( ).

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知圆![]() 和圆
和圆![]() 的极坐标方程分别是
的极坐标方程分别是![]() 和
和![]() .
.
(1)求圆![]() 和圆
和圆![]() 的公共弦所在直线的直角坐标方程;
的公共弦所在直线的直角坐标方程;
(2)若射线![]() :
:![]() 与圆
与圆![]() 的交点为O、P,与圆
的交点为O、P,与圆![]() 的交点为O、Q,求
的交点为O、Q,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com