
科目: 来源: 题型:
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
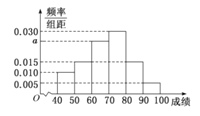
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中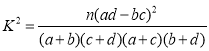 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目: 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共280分钟,请学生自主学习.区教育局为了了解高三学生网上学习情况,上课几天后在全区高三学生中采取随机抽样的方法抽取了100名学生进行问卷调查,为了方便表述把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:
类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:

(1)求100名学生中![]() ,
,![]() ,
,![]() 三类学生分别有多少人?
三类学生分别有多少人?
(2)在![]() ,
,![]() ,
,![]() 三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是
三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是![]() 类的学生人数的分布列和数学期望;
类的学生人数的分布列和数学期望;
(3)某校高三(1)班有50名学生,某天语文和数学老师计划分别在19:00—19:40和20:00—20:40在线上与学生交流,由于受校园网络平台的限制,每次只能30个人同时在线学习交流.假设这两个时间段高三(1)班都有30名学生相互独立地随机登录参加学习交流.设![]() 表示参加语文或数学学习交流的人数,当
表示参加语文或数学学习交流的人数,当![]() 为多少时,其概率最大.
为多少时,其概率最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】设以![]() 的边
的边![]() 为长轴且过点
为长轴且过点![]() 的椭圆
的椭圆![]() 的方程为
的方程为![]() 椭圆
椭圆![]() 的离心率
的离心率![]() ,
,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 和
和![]() 所在的直线分别与直线
所在的直线分别与直线![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 与
与![]() 的外接圆的面积分别为
的外接圆的面积分别为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() ,
,![]() ,侧面
,侧面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
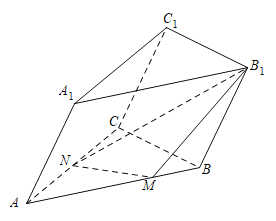
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com