
科目: 来源: 题型:
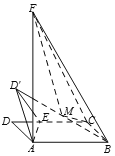
【题目】如图,已知矩形ABCD,![]() ,
,![]() ,AF⊥平面ABC,且
,AF⊥平面ABC,且![]() .E为线段DC上一点,沿直线AE将△ADE翻折成
.E为线段DC上一点,沿直线AE将△ADE翻折成![]() ,M为
,M为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 体积的最小值是________.
体积的最小值是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
,![]() ;
;
(2)函数![]() 图像与
图像与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,且在点
,且在点![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年的3月12日是植树节,某公司为了动员职工积极参加植树造林,在植树节期间开展植树有奖活动,设有甲、乙两个摸奖箱,每位植树者植树每满30棵获得一次甲箱内摸奖机会,植树每满50棵获得一次乙箱内摸奖机会,每箱内各有10个球(这些球除颜色外全相同),甲箱内有红、黄、黑三种颜色的球,其中![]() 个红球,
个红球,![]() 个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
(1)经统计,每人的植树棵数![]() 服从正态分布
服从正态分布![]() ,若其中有200位植树者参与了抽奖,请估计植树的棵数
,若其中有200位植树者参与了抽奖,请估计植树的棵数![]() 在区间
在区间![]() 内并中奖的人数(结果四舍五入取整数);
内并中奖的人数(结果四舍五入取整数);
附:若![]() ,则
,则![]() ,
,
![]() .
.
(2)若![]() ,某位植树者获得两次甲箱内摸奖机会,求中奖金额
,某位植树者获得两次甲箱内摸奖机会,求中奖金额![]() (单位:元)的分布列;
(单位:元)的分布列;
(3)某人植树100棵,有两种摸奖方法,
方法一:三次甲箱内摸奖机会;
方法二:两次乙箱内摸奖机会;
请问:这位植树者选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,以
,以![]() 为圆心过椭圆左顶点
为圆心过椭圆左顶点![]() 的圆与直线
的圆与直线![]() 相切于
相切于![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,问
,问![]() 内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列
这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,若_______,数列
,若_______,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
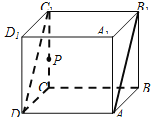
【题目】若点![]() 在平面
在平面![]() 外,过点
外,过点![]() 作面
作面![]() 的垂线,则称垂足
的垂线,则称垂足![]() 为点
为点![]() 在平面
在平面![]() 内的正投影,记为
内的正投影,记为![]() .如图,在棱长为
.如图,在棱长为![]() 的正方体
的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是棱
是棱![]() 上一动点(与
上一动点(与![]() 不重合),
不重合),![]() ,
,![]() .给出下列三个结论:①线段
.给出下列三个结论:①线段![]() 长度的取值范围是
长度的取值范围是 ;②存在点
;②存在点![]() 使得
使得![]() 平面
平面![]() ;③存在点
;③存在点![]() 使得
使得![]() .其中正确结论的序号是_______.
.其中正确结论的序号是_______.
查看答案和解析>>
科目: 来源: 题型:
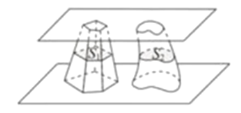
【题目】南北朝时代的伟大数学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面的面积分别为
,被平行于这两个平面的任意平面截得的两个截面的面积分别为![]() ,则“
,则“![]() 总相等”是“
总相等”是“![]() 相等”的( )
相等”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线![]() ,不与
,不与![]() 轴垂直的直线
轴垂直的直线![]() 与双曲线右支交于点
与双曲线右支交于点![]() ,
,![]() ,(
,(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),与双曲线渐近线交于点
轴下方),与双曲线渐近线交于点![]() ,
,![]() (
(![]() 在
在![]() 轴上方),
轴上方),![]() 为坐标原点,下列选项中正确的为( )
为坐标原点,下列选项中正确的为( )
A.![]() 恒成立
恒成立
B.若![]() ,则
,则![]()
C.![]() 面积的最小值为1
面积的最小值为1
D.对每一个确定的![]() ,若
,若![]() ,则
,则![]() 的面积为定值
的面积为定值
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
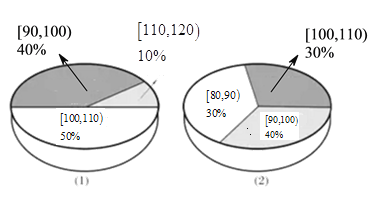
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com