
科目: 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中已知椭圆![]() ,焦点在x轴上的椭圆
,焦点在x轴上的椭圆![]() 与
与![]() 的离心率相同,且椭圆
的离心率相同,且椭圆![]() 的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆
的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)设![]() 为椭圆
为椭圆![]() 上一点(不与点A、B、C、D重合).
上一点(不与点A、B、C、D重合).
①若直线:![]() ,求证:直线l与椭圆
,求证:直线l与椭圆![]() 相交;
相交;
②记①中的直线l与椭圆C1的交点为S、T,求证![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了打击海盗犯罪,甲、乙、丙三国海军进行联合军事演习,分别派出一艘军舰A,B,C.演习要求:任何时刻军舰A、B、C均不得在同一条直线上.
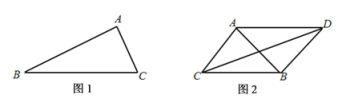
(1)如图1,若演习过程中,A、B间的距离始终保持![]() ,B,C间的距离始终保持
,B,C间的距离始终保持![]() ,求
,求![]() 的最大值.
的最大值.
(2)如图2,若演习过程中,A,C间的距离始终保持![]() ,B、C间的距离始终保持
,B、C间的距离始终保持![]() .且当
.且当![]() 变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,
变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,![]() ,与C在直线AB的两侧,求C与D间的最大距离.
,与C在直线AB的两侧,求C与D间的最大距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四面体A-BCD中,已知平面![]() 平面BCD,
平面BCD,![]() 为正三角形,
为正三角形,![]() 为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
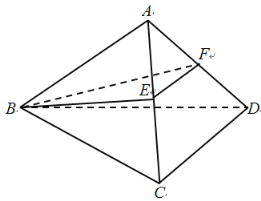
(1)求证:![]() 平面BEF;
平面BEF;
(2)求证:![]() 平面ACD.
平面ACD.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为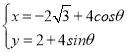 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为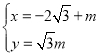 (m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(1)求曲线C的极坐标方程;
(2)直线l与曲线C相交于M,N两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某生物公司将A型病毒疫苗用100只小白鼠进行科研和临床试验,得到统计数据如表:
未感染病毒 | 感染病毒 | 总计 | |
未注射 | 10 | x | A |
注射 | 40 | y | B |
总计 | 50 | 50 | 100 |
现从所有试验的小白鼠中任取一只,取得注射疫苗小白鼠的概率为![]() .
.
(1)能否有99.9%的把握认为注射此型号疫苗有效?
(2)现从感染病毒的小白鼠中任取3只进行病理分析,记已注射疫苗的小白鼠只数为ξ,求ξ的分布列和数学期望.
附: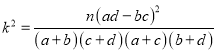
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=2px(0<p<8)的焦点为F点Q是抛物线C上的一点,且点Q的纵坐标为4,点Q到焦点的距离为5.
(1)求抛物线C的方程;
(2)设直线l不经过Q点且与抛物线交于A,B两点,QA,QB的斜率分别为K1,K2,若K1K2=﹣2,求证:直线AB过定点,并求出此定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,点E,F分别为AD,BP的中点,AD=3,AP=3![]() ,PC
,PC![]() .
.
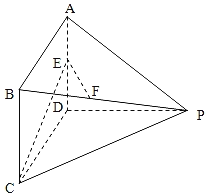
(1)求证:EF//平面PDC;
(2)若∠CDP=120°,求二面角E﹣CP﹣D的平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图.正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线OX,OY,OZ上,则在下列命题中,错误的为( )
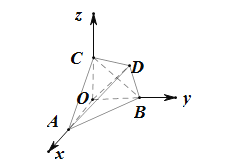
A.O﹣ABC是正三棱锥B.二面角D﹣OB﹣A的平面角为![]()
C.直线AD与直线OB所成角为![]() D.直线OD⊥平面ABC
D.直线OD⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com