
科目: 来源: 题型:
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() ,
,![]() .
.

(1)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
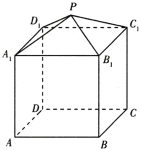
【题目】如图是一个由正四棱锥![]() 和正四棱柱
和正四棱柱![]() 构成的组合体,正四棱锥的侧棱长为6,
构成的组合体,正四棱锥的侧棱长为6,![]() 为正四棱锥高的4倍.当该组合体的体积最大时,点
为正四棱锥高的4倍.当该组合体的体积最大时,点![]() 到正四棱柱
到正四棱柱![]() 外接球表面的最小距离是( )
外接球表面的最小距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
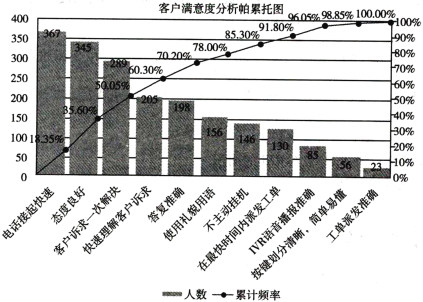
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() :
:![]() 上的点按坐标变换
上的点按坐标变换![]() ,得到曲线
,得到曲线![]() ,
,![]() 为
为![]() 与
与![]() 轴负半轴的交点,经过点
轴负半轴的交点,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,与曲线
,与曲线![]() 的交点分别为
的交点分别为![]() ,
,![]() (点
(点![]() 在第二象限).
在第二象限).
(Ⅰ)写出曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为2.
的距离为2.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)设抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 过点
过点![]() 且与抛物线
且与抛物线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() ,
,![]() 之间),点
之间),点![]() 满足
满足![]() ,求
,求![]() 与
与![]() 的面积之和取得最小值时直线
的面积之和取得最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某流行病爆发期间,某市卫生防疫部门给出的治疗方案中推荐了三种治疗药物![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
|
|
|
|
单价(单位:元) | 600 | 1000 | 800 |
治愈率 |
|
|
|
市场使用量(单位:人) | 305 | 122 | 183 |
(Ⅰ)从感染患者中任取一人,试求其一个疗程被治愈的概率大约是多少?
(Ⅱ)试估算每名感染患者在一个疗程的药物治疗费用平均是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】惰性气体分子为单原子分子,在自由原子情形下,其电子电荷分布是球对称的.负电荷中心与原子核重合,但如两个原子接近,则彼此能因静电作用产生极化(正负电荷中心不重合),从而导致有相互作用力,这称为范德瓦尔斯相互作用.今有两个相同的惰性气体原子,它们的原子核固定,原子核正电荷的电荷量为![]() ,这两个相距为
,这两个相距为![]() 的惰性气体原子组成体系的能量中有静电相互作用能
的惰性气体原子组成体系的能量中有静电相互作用能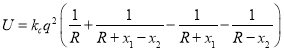 ,其中
,其中![]() 为静电常量,
为静电常量,![]() ,
,![]() 分别表示两个原子负电中心相对各自原子核的位移,且
分别表示两个原子负电中心相对各自原子核的位移,且![]() 和
和![]() 都远小于
都远小于![]() ,当
,当![]() 远小于1时,
远小于1时,![]() ,则
,则![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
薪资
岗位 |
|
|
|
|
数据开发 |
|
|
|
|
数据分析 |
|
|
|
|
数据挖掘 |
|
|
|
|
数据产品 |
|
|
|
|
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求
,求![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 恰有4个公共点,求
恰有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com