（I）完成列联表，并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关；

（Ⅱ）某课题研究小组假设各组男女同学分差服从正态分布，首先根据前20组男女同学的分差确定和，然后根据后面5组同学的分差来检验模型，检验方法是：记后面5组男女同学分差与的差的绝对值分别为，若出现下列两种情况之一，则不接受该模型，否则接受该模型.①存在；②记满足的i的个数为k，在服从正态分布的总体（个体数无穷大）中任意取5个个体，其中落在区间内的个体数大于或等于k的概率为P，.

试问该课题研究小组是否会接受该模型.

参考公式和数据：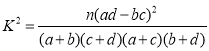

，；若，有，.

【题目】已知函数（，且，e为自然对数的底）.

（I）求函数的单调区间

（Ⅱ）若函数在有两个不同零点，求a的取值范围.

【题目】已知双曲线上任意一点（异于顶点）与双曲线两顶点连线的斜率之积为.

（I）求双曲线渐近线的方程；

（Ⅱ）过椭圆上任意一点P（P不在C的渐近线上）分别作平行于双曲线两条渐近线的直线，交两渐近线于两点，且，是否存在使得该椭圆的离心率为，若存在，求出椭圆方程：若不存在，说明理由.

【题目】如图所示，四棱柱中，底面是以为底边的等腰梯形，且.

（I）求证：平面平面；

（Ⅱ）若，求直线AB与平面所成角的正弦值.

【题目】已知等差数列的公差为，前n项和为，且满足____________.（从①）；②成等比数列；③，这三个条件中任选两个补充到题干中的横线位置，并根据你的选择解决问题）

（I）求；

（Ⅱ）若，求数列的前n项和.

【题目】已知正四棱锥中，是边长为3的等边三角形，点M是的重心，过点M作与平面PAC垂直的平面，平面与截面PAC交线段的长度为2，则平面与正四棱椎表面交线所围成的封闭图形的面积可能为______________.（请将可能的结果序号填到横线上）①2；②；③3； ④.

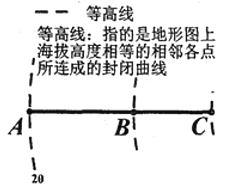
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式，使用提水吊杆——桔槔，后发展成辘轳.19世纪末，由于电动机的发明，离心泵得到了广泛应用，为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影，在A处测得B处的仰角为37度，在A处测得C处的仰角为45度，在B处测得C处的仰角为53度，A点所在等高线值为20米，若BC管道长为50米，则B点所在等高线值为( )（参考数据）

A.30米B.50米C.60米D.70米

【题目】平面直角坐标系xOy中，抛物线E顶点在坐标原点，焦点为.以坐标原点为极点，x轴非负半轴为极轴建立极坐标系.

（Ⅰ）求抛物线E的极坐标方程；

（Ⅱ）过点倾斜角为的直线l交E于M，N两点，若，求.

【题目】已知椭圆，过点的两条不同的直线与椭圆E分别相交于A，B和C，D四点，其中A为椭圆E的右顶点.

（1）求以AB为直径的圆的方程；

（2）设以AB为直径的圆和以CD为直径的圆相交于M，N两点，探究直线MN是否经过定点，若经过定点，求出定点坐标；若不经过定点，请说明理由.

【题目】已知等差数列的公差为，前n项和为，且满足____________.（从①）；②成等比数列；③，这三个条件中任选两个补充到题干中的横线位置，并根据你的选择解决问题）

（I）求；

（Ⅱ）若，求数列的前n项和.