
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为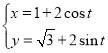 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,且
,且![]() 的面积不超过
的面积不超过![]() ,求直线
,求直线![]() 的倾斜角的取值范围.
的倾斜角的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学长期坚持贯彻以人为本,因材施教的教育理念,每年都会在校文化节期间举行“数学素养能力测试”和“语文素养能力测试”两项测试,以给学生课外兴趣学习及辅导提供参考依据.成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级(等级
五个等级(等级![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为
分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为![]() 的考生有3人.
的考生有3人.
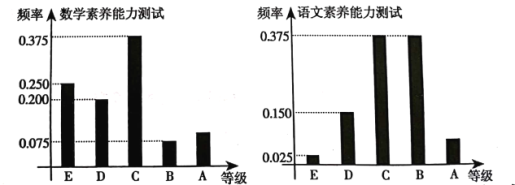
(1)求该班“数学素养能力测试”的科目平均分以及“数学素养能力测试”科目成绩为![]() 的人数;
的人数;
(2)若该班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.从这9人中随机抽取三人,设三人的成绩之和为![]() ,求
,求![]() .
.
(3)从该班得分大于7分的9人中选3人即甲,乙,丙组队参加学校内的“数学限时解题挑战赛”.规则为:每队首先派一名队员参加挑战赛,在限定的时间,若该生解决问题,即团队挑战成功,结束挑战;若解决问题失败,则派另外一名队员上去挑战,直至派完队员为止.通过训练,已知甲,乙,丙通过挑战赛的概率分别是![]() ,
,![]() ,
,![]() ,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目: 来源: 题型:
【题目】山东省2020年高考将实施新的高考改革方案.考生的高考总成绩将由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、历史、政治、地理6科中选择3门作为选考科目,语、数、外三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级。参照正态分布原则,确定各等级人数所占比例分别为
共8个等级。参照正态分布原则,确定各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .等级考试科目成绩计入考生总成绩时,将
.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
举例说明.
某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分为:
等级的转换分区间为61~70,那么该同学化学学科的转换分为:
设该同学化学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .
.
四舍五入后该同学化学学科赋分成绩为67.
(1)某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布![]() .
.
(i)若小明同学在这次考试中物理原始分为84分,等级为![]() ,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
(ii)求物理原始分在区间![]() 的人数;
的人数;
(2)按高考改革方案,若从全省考生中随机抽取4人,记![]() 表示这4人中等级成绩在区间
表示这4人中等级成绩在区间![]() 的人数,求
的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面PAC⊥平面ABC,![]() 是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,
是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,![]() .
.

(1)设G是OC的中点,证明:![]() ∥平面
∥平面![]() ;
;
(2)证明:在![]() 内存在一点M,使FM⊥平面BOE,求点M到OA,OB的距离.
内存在一点M,使FM⊥平面BOE,求点M到OA,OB的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,固定边
,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 、
、![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,
取得最小值时,![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.


由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目: 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
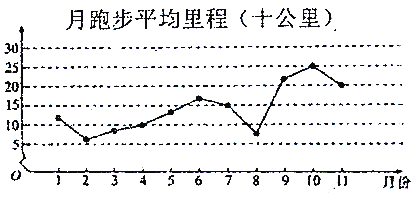
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com