
科目: 来源: 题型:
【题目】已知椭圆![]() 的标准方程是
的标准方程是![]() ,设
,设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 做
做![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() ,
,![]() .
.
(1)证明:线段![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(2)当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海、香港、澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如图.
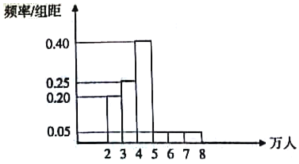
(1)求这100天中,客流量超过4万的频率;
(2)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() ,则双曲线的渐近线斜率的平方的取值范围是( )
,则双曲线的渐近线斜率的平方的取值范围是( )
A.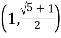 B.
B.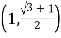
C.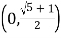 D.
D.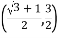
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点
),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() 可,试判断曲线
可,试判断曲线![]() 和
和![]() 的位置关系;
的位置关系;
(2)若曲线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 两点,且
两点,且![]() ,满足
,满足![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的标准方程是
的标准方程是![]() ,设
,设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 做
做![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() ,
,![]() .
.
(1)证明:线段![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(2)当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.
2019年从五月一日开始的连续100天客流量频率分布直方图如下
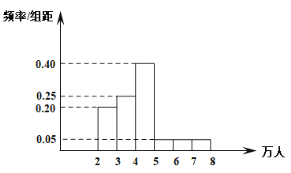
(1)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
(2)设这100天中客流量超过5万人次的有![]() 天,从这
天,从这![]() 天中任取两天,设
天中任取两天,设![]() 为这两天中客流量超过7万人的天数.求
为这两天中客流量超过7万人的天数.求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,若椭圆的长轴长等于
,若椭圆的长轴长等于![]() 的直径,且
的直径,且![]() ,
,![]() 成等差数列
成等差数列
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 、
、![]() 是椭圆
是椭圆![]() 上不同的两点,线段
上不同的两点,线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() ,试求点
,试求点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数的期望和方差.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式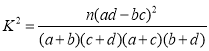 其中
其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com