
科目: 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
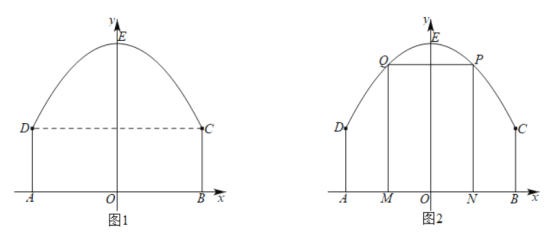
(1)求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
(2)如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为过焦点
为过焦点![]() 且垂直于
且垂直于![]() 轴的抛物线
轴的抛物线![]() 的弦,已知以
的弦,已知以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
(1)求![]() 的值及该圆的方程;
的值及该圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
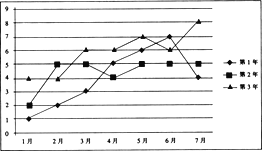
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 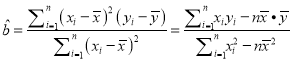 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合,已求得:用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() );
);
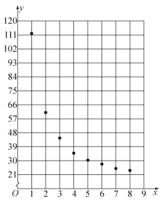
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本.
参考数据:![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: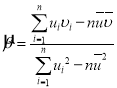 ,
,![]() ,相关系数
,相关系数 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们听到的美妙弦乐,不是一个音在响,而是许多个纯音的合成,称为复合音.复合音的响度是各个纯音响度之和.琴弦在全段振动,产生频率为![]() 的纯音的同时,其二分之一部分也在振动,振幅为全段的
的纯音的同时,其二分之一部分也在振动,振幅为全段的![]() ,频率为全段的2倍;其三分之一部分也在振动,振幅为全段的
,频率为全段的2倍;其三分之一部分也在振动,振幅为全段的![]() ,频率为全段的3倍;其四分之一部分也在振动,振幅为全段的
,频率为全段的3倍;其四分之一部分也在振动,振幅为全段的![]() ,频率为全段的4倍;之后部分均忽略不计.已知全段纯音响度的数学模型是函数
,频率为全段的4倍;之后部分均忽略不计.已知全段纯音响度的数学模型是函数![]() (
(![]() 为时间,
为时间,![]() 为响度),则复合音响度数学模型的最小正周期是_____________.
为响度),则复合音响度数学模型的最小正周期是_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
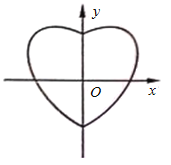
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com