
科目: 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,点P是上底面A1B1C1D1内一点,且AP∥平面EFDB,则cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中曲线C的参数方程为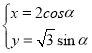 (
(![]() 为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为
为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为![]() .
.
(I)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(II)若M为曲线C上一动点,求点M到直线l的最小距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
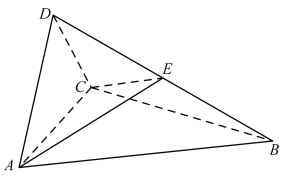
(I)证明:平面![]() 平面ABC;
平面ABC;
(II)点E在BD上,若平面ACE把三棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() ,
,![]() 分别是其左、右焦点,过
分别是其左、右焦点,过![]() 的直线l与椭圆C交于A,B两点,且椭圆C的离心率为
的直线l与椭圆C交于A,B两点,且椭圆C的离心率为![]() ,
,![]() 的内切圆面积为
的内切圆面积为![]() ,
,![]() .
.
(I)求椭圆C的方程;
(II)若![]() 时,求直线l的方程
时,求直线l的方程
查看答案和解析>>
科目: 来源: 题型:
【题目】给出以下四个命题:
①数列![]() 为等差数列的充要条件是其通项公式为n的一次函数.
为等差数列的充要条件是其通项公式为n的一次函数.
②在面积为S的![]() 的边AB上任取一点P,则
的边AB上任取一点P,则![]() 的面积大于
的面积大于![]() 的概率为
的概率为![]() .
.
③将多项式![]() 分解因式得
分解因式得![]() ,则
,则![]() .
.
④若那么由![]() ,那么由
,那么由![]() 以及x轴所围成的图形一定在x轴下方.
以及x轴所围成的图形一定在x轴下方.
其中正确命题的序号为_____________(把所有正确命题的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com