
科目: 来源: 题型:
【题目】新型冠状病毒蔓延以来,世界各国都在研制疫苗,某专家认为,某种抗病毒药品对新型冠状病毒具有抗病毒、抗炎作用,假如规定每天早上7:00和晚上7:00各服药一次,每次服用该药药量700毫克具有抗病毒功效,若人的肾脏每12小时从体内滤出这种药的70%,该药在人体内含量超过1000毫克,就将产生副作用,若人长期服用这种药,则这种药__________(填“会”或者“不会”)对人体产生副作用.
查看答案和解析>>
科目: 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在
猜想”,是德国数学家洛萨克拉茨在![]() 年世界数学家大会上公布的一个猜想:任给一个正整数
年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘
为奇数就将它乘![]() 加
加![]() ,不断重复这样的运算,经过有限步后,最终都能够得到
,不断重复这样的运算,经过有限步后,最终都能够得到![]() ,得到
,得到![]() 即终止运算,己知正整数
即终止运算,己知正整数![]() 经过
经过![]() 次运算后得到
次运算后得到![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]() 或
或![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() ,二面角
,二面角![]() 、
、![]() 、
、![]() 的大小均为
的大小均为![]() ,设三棱锥
,设三棱锥![]() 的外接球球心为
的外接球球心为![]() ,直线
,直线![]() 交平面
交平面![]() 于点
于点![]() ,则三棱锥
,则三棱锥![]() 的内切球半径为_______________,
的内切球半径为_______________,![]() __________
__________
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,且x=0是f(x)的极值点.
,且x=0是f(x)的极值点.
(1)求f(x)的最小值;
(2)是否存在实数b,使得关于x的不等式ex<bx+f(x)在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为11万元/辆和8万元/辆的A,B两款车型,根据以往这两种出租车车型的数据,得到两款出租车型使用寿命频数表如表:
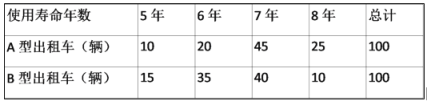
(1)填写如表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车有关?
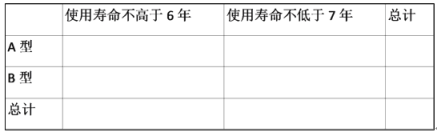
(2)以频率估计概率,从2020年生产的A和B的车型中各随机抽1车,以X表示这2车中使用寿命不低于7年的车数,求X的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租每年上交公司6万元,其余维修和保险等费用自理,假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这100辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
参考公式: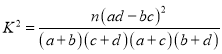 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
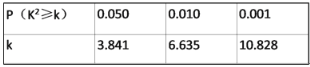
查看答案和解析>>
科目: 来源: 题型:
【题目】如图已知![]() ,
,![]() ,
,![]() 、
、![]() 分別为
分別为![]() 、
、![]() 的中点
的中点![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
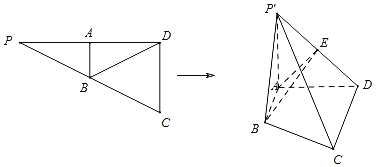
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,
的方向相同时,![]() 的正视图为直角三角形,求此时二面角
的正视图为直角三角形,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com