
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时,![]() 的面积为
的面积为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经点
经点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
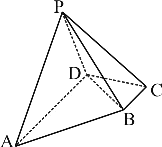
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】实现国家富强.民族复兴.人民幸福是“中国梦”的本质内涵.某商家计划以“全民健身促健康,同心共筑中国梦”为主题举办一次有奖消费活动,此商家先把某品牌乒乓球重新包装,包装时在每个乒乓球上印上“中”“国”“梦”三个字样中的一个,之后随机装盒(1盒4个球),并规定:若顾客购买的一盒球印的是同一个字,则此顾客获得一等奖;若顾客购买的一盒球集齐了“中”“国”二字且仅有此二字,则此顾客获得二等奖;若顾客购买的一盒球集齐了“中”“国”“梦”三个字,则此顾客获得三等奖,其它情况不设奖,则顾客购买一盒乒乓球获奖的概率是_____________.
查看答案和解析>>
科目: 来源: 题型:
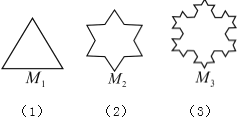
【题目】分形几何是一门以不规则几何形态为研究对象的几何学,科赫曲线是比较典型的分形图形,1904年瑞典数学家科赫第一次描述了这种曲线,因此将这种曲线称为科赫曲线.其生成方法是:(I)将正三角形(图(1))的每边三等分,以每边三等分后的中间的那一条线段为一边,向形外作等边三角形,并将这“中间一段”去掉,得到图(2);(II)将图(2)的每边三等分,重复上述的作图方法,得到图(3);(Ⅲ)再按上述方法继续做下去……,设图(1)中的等边三角形的边长为1,并且分别将图(1)、图(2)、图(3)、…、图(n)、…中的图形依次记作![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,设
,…,设![]() 的周长为
的周长为![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%小学初中高中学段的学生进行调查,则抽取的样本容量、抽取的高中生家中参与“家务劳动”的人数分别为( )
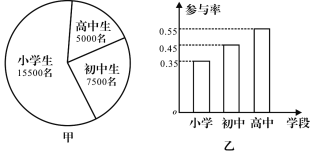
A.2750,200B.2750,110C.1120,110D.1120,200
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)某中学理学社为了吸收更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参加.社团活动积极分子甲同学参加了活动.
①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.
②理学社设置了第![]() (
(![]() )个月中签的名额为
)个月中签的名额为![]() ,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参加,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第![]() (
(![]() )个月中签的概率为
)个月中签的概率为![]() ,活动进行了
,活动进行了![]() 个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于
个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于![]() 个月.
个月.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,以短轴长为直径的圆
,且以原点为圆心,以短轴长为直径的圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与圆
,且与圆![]() 没有公共点,设
没有公共点,设![]() 为椭圆
为椭圆![]() 上一点,满足
上一点,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
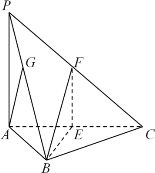
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com